Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 87
87- É feito o modelo de um transdutor com uma fonte de corrente e uma resistência em paralelo . A medição da corrente nos terminais da fonte resulta em quando for usado um amperímetro com resistência interna de .
Se o acréscimo de um resistor de entre os terminais da fonte faz a leitura no amperímetro cair para , calcule e .
Qual será a leitura do amperímetro se a resistência entre os terminais da fonte for alterada para ?
Passo 1
Vamos calcular o valor da fonte de corrente e da resistência interna quando temos uma resistência interna de .
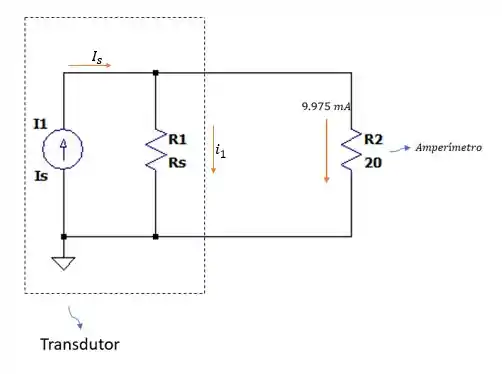
Fazendo a somatória das correntes no circuito temos que:
Pois a tensão em cima do resistor é a mesma do resistor de .
Porém precisaremos de mais dados para poder calcular e e para isso temos os dados da letra que nos dá o seguinte circuito.
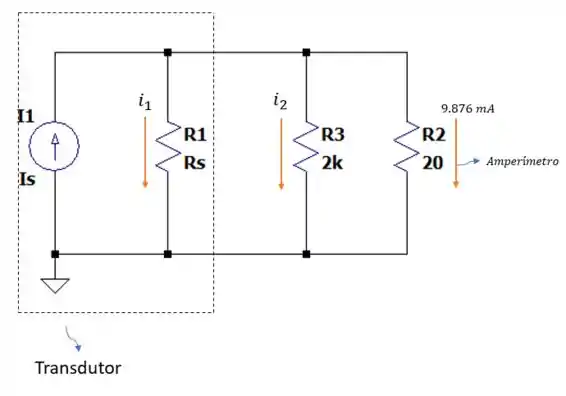
Uma vez que a carga de é colocada entre os terminais da fonte de corrente.
Fazendo a somatória das correntes nesse cricuito temos:
Passo 2
Dessa forma vamos resolver o sistema para encontrar e :
Diminuindo a primeira equação pela segunda temos:
Dessa forma valerá:
Passo 3
Agora com esses valores do equivalente de Thévenin vamos alterar a carga de para e ver o que acontece com a leitura no amperímetro.
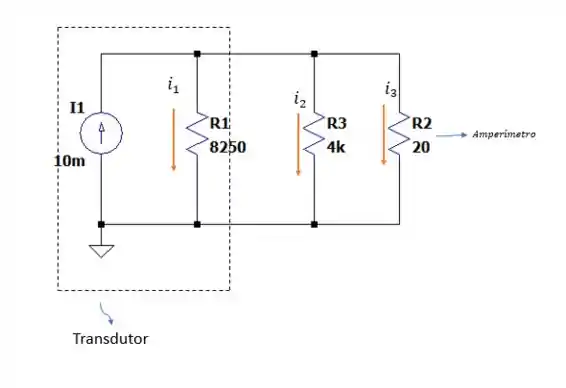
Fazendo a somatória das correntes temos:
Pois a mesma tensão aplicado no amperímetro tambem será aplicado em todos os outros resistores e é a corrente que passa pelo amperímetro, logo: