Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 5.Problemas - Ex. 26
Calcule o equivalente de Norton do circuito a esquerda dos terminais a-b e use o resultado para calcular a potência entregue ao resistor de 6kΩ.
Passo 1
Iae, meus queridos!! Td certinho?
Vamos analisar o circuito dado.
Sabemos que , portanto a tensão no resistor de conectado ao terminal negativo do Amp Op, é , aplicando a Lei de Ohm, podemos encontrar a corrente gerada pela fonte.
Sabemos também que a corrente que entra nos terminais + e – do Amp Op é 0, então a corrente no resistor de também é , dessa forma, aplicando Lei de Ohm, teremos a tensão .
Passo 2
Calculando a Resistência equivalente à direita de , podemos calcular a corrente à direita de .
Aplicando o método de divisão de corrente teremos a tensão em a-b.
Aplicando Lei de Ohm.
Nesse caso, nosso será nosso , retirando o resistor de dos terminais ab e os curto-circuitando, analisamos que será nosso
Só nos falta calcular e montar o circuito.
Portanto, nosso circuito ficará assim:
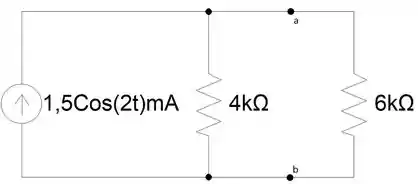
Passo 3
A potência entregue ao resistor é:
Iae, foi tranquilo? Bora pra mais uma!