Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 3.Problemas - Ex. 7
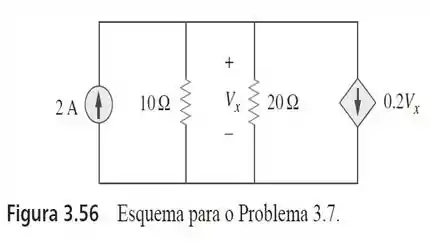
7. Aplique a análise nodal para determinar no circuito da figura
Passo 1
Bom! Uma coisa importante a se saber pra resolver esse tipo de problema é que a corrente elétrica irá sempre se deslocar de um ponto de maior potencial pra um de menor potencial.
Depois desse maravilhosa dica, nossa próxima ação é dar nomes aos bois. Esse circuito da figura do enunciado tá parecendo meio xoxo, né não? Por isso, o que devemos fazer é redesenhar esse circuito de uma forma mais compreensível para realizarmos a nossa análise nodal. Vamos lá...
Aqui está nossa obra de arte:
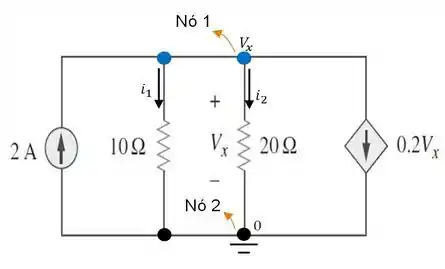
Passo 2
Nesse circuito os elementos de cada ramo estão ligado em paralelo. E como podemos ver no esboço anterior, ele possui nós, sendo que o nó de número está ligado à terra e portanto, tem potencial nulo.
Com isso, aplicando a para o nó , temos que:
Uma vez que a corrente sai sempre do maior para o menor potencial, vamos determinar agora as equações das correntes em relação às tensões em cada resistor:
E substituindo em seguida essas fórmulas, na relação que obtivemos do , chegamos à seguinte equação:
Que iremos resolver agora...
Pronto! Missão cumprida!