Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 4.Problemas - Ex. 14

Usando a analise nodal, calcule i.

Passo 1

E aí pessoal, tudo bem?

Essa questão pede a corrente i no seguinte circuito:

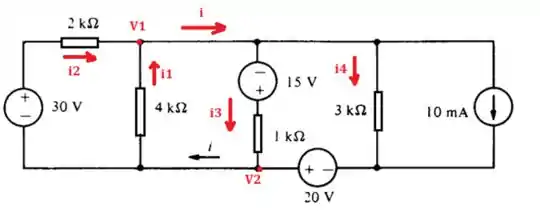
Beleza, agora vamos equacionar os nós!

Passo 2

No nó 1, temos:

10 + i_4 + i_3 = i

No nó 2, temos:

i_2 + i_1 = i

Somando as duas, temos:

i_1 + i_2 = i_3 + i_4 + 10

Agora, vamos achar as equações da 3 malhas.

Na malha da esquerda:

30 = 2 i_2 - 4 i_1

i_2 = 15 + 2 i_1

Na malha do meio:

15 = i_3 + 4 i_1

i_3 = 15 - 4 i_1

Na malha da direita, temos:

20 = 15 - i_3 + 3 i_4

Substituindo i_3 :

20 = 4 i_1 + 3 i_4

i_4 = (20 - 4 i_1)/(3)

Passo 3

Show! Agora é só substituir i_2 , i_3 e i_4 na seguinte equação:

i_1 + i_2 = i_3 + i_4 + 10

i_1 + 15 + 2 i_1 = 15 - 4 i_1 + (20 - 4 i_1)/(3) + 10

21 i_1 = 20 - 4 i_1 + 30

25 i_1 = 50

i_1 = 2 m A

Como i = i_1 + i_2 e i_2 = 15 + 2 i_1 temos:

i = 15 + 3 i_1

i = 15 + 6

i = 21 m A

Resposta

i = 21 m A

Exercícios de Livros Relacionados

Calcule a potência entregue para o resistor de 20 Ω, usando a análise nodal.
Usando a analise nodal, calcule i_1 e i_2 .
Usando a análise nodal, calcule i.
Usando a analise nodal, calcule v_1 e v_2 .
Usando a analise nodal, calcule v.