Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 3.Problemas - Ex. 6
Para cada um dos circuitos mostrados na Figura P3.4,
a) determine a resistência equivalente vista pela fonte,
b) determine a potência fornecida pela fonte
Passo 1
Iae, meus queridos! Td certinho??
Muito bacana essa questão, muito importante o conhecimento desses conceitos pra vida de um futuro engenheiro 😉.
Na figura P3.4(a), temos o seguinte circuito:
Vemos que os resistores de 36 e 18 ohms, estão em paralelo e a resultante dessa associação em paralelo, está em série com o resistor de 24 ohms, ou seja
A potencia fornecida pela fonte, será dada como
Passo 2
O circuito da figura P3.4(b) pode ser um pouco mais complexo, por isso, vamos explicar mais devagar.
Primeiro temos a seguinte associação em paralelo.
Dada por
Após isso, formamos uma outra associação, dada por
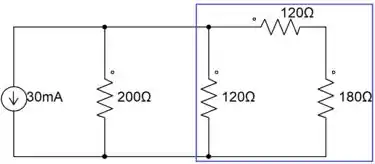
Uma associação em série de 120 e 180 ohms, que está em paralelo com 120 ohms, ou seja
Por fim, essa resistência equivalente será associada em paralelo com a resistência de 200 ohms.
A potência gerada pela fonte, é dada como
Passo 3
O circuito da figura P3.4(c) é dado por
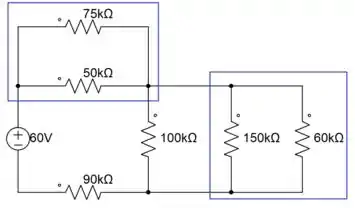
Podemos calcular duas associações em paralelo ao mesmo tempo (destacadas), onde
Dessa forma temos um novo circuito equivalente
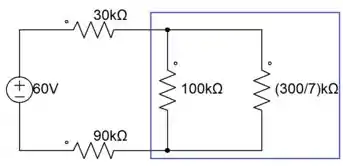
Por fim, temos uma associação em paralelo com essa resultante associada em série com os resistores de 30k e 90k ohms
A potência fornecida pela fonte é dada por
Passo 4
No ultimo circuito, da figura P3.4(d) temos 3 associações logo de cara, destacadas na imagem
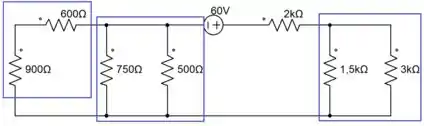
Com isso temos um circuito mais simplificado, dado por
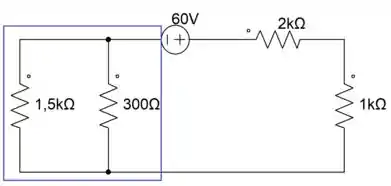
A associação destacada, está em série com os resistores de 2k e 1k ohms, então
Por fim, a potência é dada por
Bacana, né? Muito legal essa questão! 😎
Resposta
(a) ; ; ;
(b) ; ; ;