Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 3.Problemas - Ex. 23
Examine o circuito da Figura P3.3(a)
a) Use a divisão de tensão para determinar a tensão que percorre o resistor de , positiva na parte superior.
b) Usando o resultado de (a) e a divisão de tensão, determine a tensão nos terminais do resistor de , positiva à esquerda.
Passo 1
Uhuuu! Vamos pra mais uma questão nesta nova seção que se inicia!!!
Para refrescar um pouco nossa memória, vamos colocar aqui o circuito em questão:
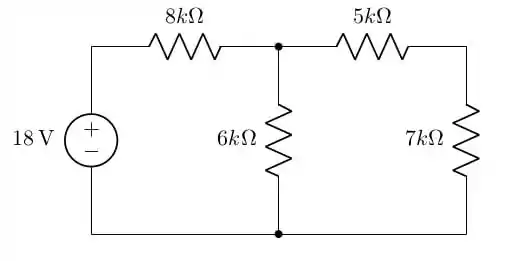
Passo 2
a)
Para resolver esta questão, vamos começar simplificando o circuito dado. Percebemos primeiro que os resistores de e estão em série:
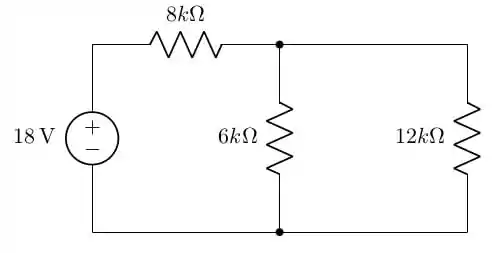
Agora, vemos que os resistores de e estão em paralelo, e sua resistência equivalente será dada por:
E o circuito é simplificado para
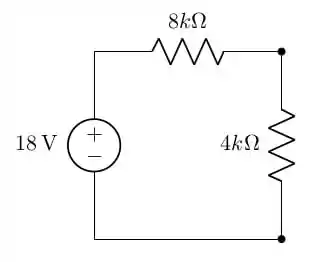
Aqui temos que fazer a seguinte observação. A tensão em cima do resistor de é a mesma em cima do resistor equivalente de e que por sua vez é a mesma em cima do resistor original de . Por isso, podemos calcular o divisor de tensão com este circuito reduzido. Perceba que isso é totalmente diferente de usar diretamente o resistor de no cálculo do divisor de tensão.
Assim:
Passo 3
b)
Aqui vamos usar o mesmo princípio que foi descrito no passo anterior, ou seja, a tensão no resistor de é a mesma no resistor equivalente de . Então, usando este raciocínio e o resultado do item anterior, podemos concluir que
Partiu próxima questão!
Resposta
a)
b)