Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 3.Problemas - Ex. 63

Para o circuito mostrado na Figura P3.63, determine (a) i 1, (b) v, (c) i 2 e (d) a potência fornecida pela fonte de tensão.

Passo 1

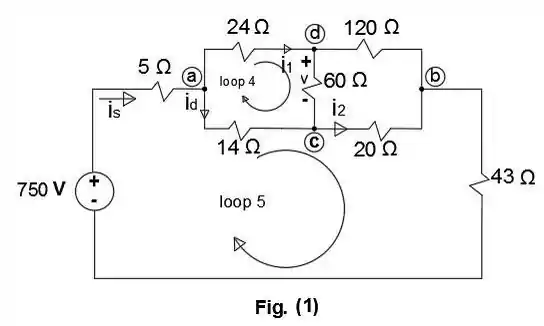
Convertendo adcb (24, 60,120) Ω de estrela para delta

R a = 24 ∙ 120 + 120 ∙ 60 + 60 ∙ 24 24

R a = 480   Ω

R b = 24 ∙ 120 + 120 ∙ 60 + 60 ∙ 24 120

R b = 96   Ω

R c = 24 ∙ 120 + 120 ∙ 60 + 60 ∙ 24 60

R c = 192   Ω

R a | | 20 Ω a resistência equivalente é:

480 ∙ 20 480 + 20 = 19.2   Ω

R b | | 14 Ω a resistência equivalente é:

96 ∙ 14 96 + 14 = 12.2   Ω

Passo 2

19.2 + 12.2 | | R c a resistência equivalente para eles é de:

31.4   | |   192

31.4 ∙ 192 31.4 + 192 = 27   Ω

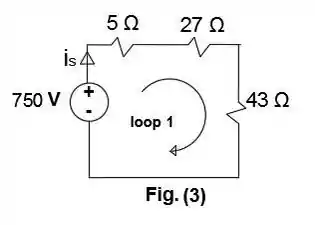
Na figura 3 utilizando da Lei de Kirchhof no Loop 1:

- 750 + i s 5 + 27 + 43 = 0

i s = 750 75

i s = 10 A

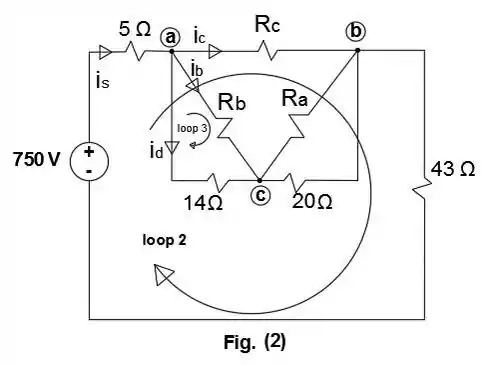
Da figura (2) utilizando Lei de de Kirchhof no Loop 2:

- 750   +   ( i s 5 )   +   ( i c R c )   +   ( i c 43 )   =   0

- 750   +   ( 10   ∙ 5 )   +   ( i c     ∙ 192 )   +   ( 10   ∙ 43 )   =   0

i c   =   1.4   A

Na figura (2) usando novamente a Lei de Kirchhof no nó a:

i s   -   i c   -   i b   -   i d   =   0

10   -   1.4   -   i b   -   i d   =   0

i b   +   i d   =   8.6   - >   ( 1 )

da figura (2) utilizando a Lei de Kichhof no Loop 3:

( R b   ∙ i b )   -   ( 14   ∙ I d )   =   0

96 i b   -   14 i d   =   0   - >   ( 2 )

resolvendo (1) e (2)

i d   =   7.5   A

i b   =   1.1   A

da figura (1) utilizando Lei de Kirchhof no nó a:

i 1   +   i d   -   i s   =   0

i 1   +   7.5   -   10   = 0

i 1   =   2.5   A

da figura (1) equacionando agora o Loop 4:

24 i 1   +   v   -   14 i d   =   0

( 24   ∙ 2.5 )   +   v   -   ( 14   ∙ 7.5 )   =   0

v   =   45   V

Passo 3

Da figura (1) e usando novamente a Lei de Kirchhof no Loop 5:

- 750   +   ( i s ∙ 5 )   +   ( i d ∙ 14 )   +   ( i 2 ∙ 20 )   +   ( i s ∙ 43 )   =   0

750   +   ( 10   ∙ 5 )   +   ( 7.5   ∙ 14 )   +   20 i 2   +   ( 10 ∙ 43 )   =   0

i 2   =   8.25   A

a potência é dada por:

P   =   v s i s   =   750   ∙ 10   =   7500   W

Resposta

  1. 2.5 A
  2. 45 V
  3. 8.25 A
  4. 7500

Exercícios de Livros Relacionados

Calcule a potência absorvida pelo resistor de 12Ω.
Calcule i_1 , i_2 e v .
Na Fig. 2.14(a), v=16 e - tV , v 2 = 4 e - t , R 1 = 24Ω . Calcule (a) R 2 , (b) a potência instantânea entregue.
Calcule (a) a resistência equivalente vista pela fonte, (b) a corrente i , (c) a potência entregue pela fonte, (d) v 1 , (e) v 2 e (f) 0 valor nominal mínimo (wattagem) necessário para 0 resistor de 4
Se i 1 = 9 e i 2 = 6 na Fig. 2.17 (a) calcule a relação R 2 // R 1 .