Calcule V e i.
Passo 1
Dado o circuito:
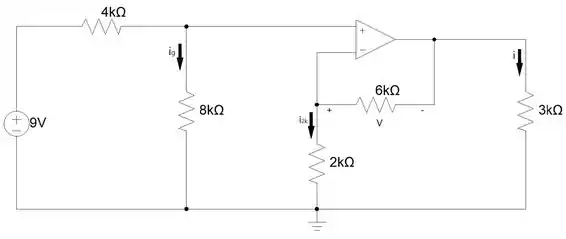
A primeira parte da resolução é encontrar a tensão do Amp Op, pra isso temos que calcular . Como a corrente no terminal + do Amp Op é 0, podemos imaginar a malha da esquerda como sendo um circuito fechado.
Aplicando a Lei de Ohm, facilmente podemos calcular através da tensão da fonte e da resistência equivalente em série
Podemos afirmar que a tensão no resistor 8 é a mesma tensão no Amp Op.
Passo 2
Como aprendemos nesse capítulo em Amp Op, então temos o valor de e podemos encontrar a corrente q passa pelo resistor de .
A corrente encontrada , é a mesma que passa no resistor de 6kΩ, então podemos usa-la para calcular a tensão V.
Obs: O valor negativo se dá por conta do sentido da corrente.
Passo 3
Por fim, basta somar e para encontrar a tensão no resistor de e aplicar a Lei de Ohm para encontrar a corrente i.