Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.Problemas - Ex. 33

Calcule v para t>0, se v (0) = 2 V e (a) v_g = 4 V , (b) v_g = 6 e^(- t) V e (c) v_g = 6 e^(- 3 t) V .

Passo 1

Fala, pessoal. Tudo tranquilo? Vocês estão mandando muito nas questões. Mas, vamos continuar praticando. Olha só esse circuito RC, a questão nos pede a tensão que está passando no capacitor de (1)/(12) F . Vamos fazer juntinhos e arrasar! 💪

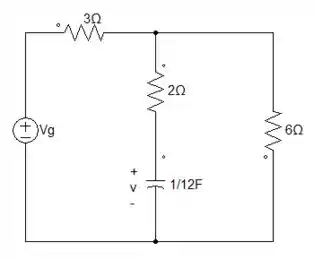
Bom, pessoal, nessa questão teremos que achar nossa EDO quando v (0) = 2 V , o que nos dará a resposta natural desse circuito. E para acharmos a resposta forçada? 🤔Vamos pegar os valores propostos do v_g e utilizar na EDO. Vamos lá?!

Para começar, vamos adotar uma tensão no nó a e chamaremos ela de V_1 .

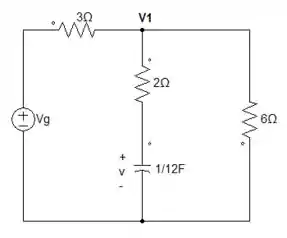
Belezinha! Agora, podemos fazer análise nodal nesse nó. Mas, antes vamos definir mais uma coisinha...vamos dizer que a corrente que passa no resistor de 6Ω é i_1 e a corrente que passa no resistor de 3Ω é i_2 . Show de bola! Já temos tudo que precisamos. Partiu 😊.

Temos que:

i_1 = (V_1)/(6)

i_2 = (v_g - V_1)/(3)

i_c = C * (d v)/(d t)

V_1 = v + 2 i_c

Vamos fazer LKC

i_2 = i_c + i_1

(v_g - V_1)/(3) = (1)/(12) * (d v)/(d t) + (V_1)/(6)

(v_g)/(3) = (1)/(12) * (d v)/(d t) + (V_1)/(2)

(v_g)/(3) = (1)/(12) * (d v)/(d t) + (v + 2 i_c)/(2)

(v_g)/(3) = (1)/(12) * (d v)/(d t) + (v)/(2) + (1)/(12) * (d v)/(d t)

(v_g)/(3) = (1)/(6) * (d v)/(d t) + (v)/(2)

v_g = (1)/(2) * (d v)/(d t) + (3 v)/(2)

Boa, pessoal! Chegamos na EDO. Vamos resolvê-la.

0 = (1)/(6) * (d v)/(d t) + (v)/(2)

- (1)/(2) = (1)/(6) * (d v)/(d t) * (v)/(2)

- 3 d t = (d v)/(v)

v_c n (t) = A e^(- 3 t) V

Passo 2

Muito bom! Feito isso, iremos partir para as respostas forçadas. Na letra (a) nos pede para sabermos quando v_g = 4 V . Vamos lá!

v_g = (1)/(2) * (d v)/(d t) + (3 v)/(2)

4 = (1)/(2) * (d v)/(d t) + (3 v)/(2)

v_c f = C

C = 4

v_c f (t) = A e^(- 3 t) V + C

2 = A e^(- 3 t) V + 4

A = - 2

v_c f (t) = - 2 e^(- 3 t) V + 4 V

Passo 3

Massa! Tá tirando onda.

Se liga! Vamos repetir o mesmo processo na letra (b) quando v_g = 6 e^(- t) V .

v_g = (1)/(2) * (d v)/(d t) + (3 v)/(2)

6 e^(- t) = (1)/(2) * (d v)/(d t) + (3 v)/(2)

v_c f = C

C = 6

v_c f (t) = A e^(- 3 t) V + C

2 = A e^(- 3 t) V + 6

A = - 4

v_c f (t) = - 4 e^(- 3 t) V + 6 e^(- t) V

Passo 4

Muito bom, galerinha! Já pegou o jeito?! Para terminar, vamos fazer um pouco diferente dessa vez, porque as tensões vão possuir a mesma raiz. Se liga aí 😉

v_c f (t) = B e^(- 3 t)

v_c f 1 (t) = B e^(- 3 t) - 3 B e^(- 3 t)

6 e^(- 3 t) = (1)/(2) (B e^(- 3 t) - 3 B e^(- 3 t)) + (3)/(2) B e^(- 3 t)

6 e^(- 3 t) = (B e^(- 3 t))/(2)

B=12

v_c f (t) = A e^(- 3 t) + 12 e^(- 3 t)

v (0) = 2 = A

v_c f (t) = 2 e^(- 3 t) + 12 e^(- 3 t) V

Resposta

v_c f (t) = - 2 e^(- 3 t) V + 4 V

v_c f (t) = - 4 e^(- 3 t) V + 6 e^(- t) V

v_c f (t) = 2 e^(- 3 t) + 12 e^(- 3 t) V

Exercícios de Livros Relacionados

No projeto de um circuito de comutação de sinais foi constatado que um capacitor de 100 mF era necessário para uma constante de tempo de 3 ms. Qual é o valor do resistor necessário para o circuito?
A chave na Figura 7.141 abre em t = 0. Use o PSpice ou MultiSim para determinar v(t) para t0.
Repita o Problema 7.49 usando o PSpice ou MultiSim.
Um circuito R C é formado por uma associação em série entre uma fonte de 120V , uma chave, um resistor de 34M Ω e um capacitor de 15μ F . O circuito é usado para estimar a velocidade de um cavalo corr
A Figura 7.145 é mostrado um circuito oscilador de relaxação simples. A lâmpada de neon acende quando sua tensão atinge 75V e apaga quando sua tensão cai para 30V . Sua resistência é 120Ω quando acesa