Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 85

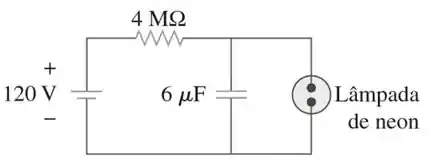
A Figura 7.145 é mostrado um circuito oscilador de relaxação simples. A lâmpada de neon acende quando sua tensão atinge 75   V   e apaga quando sua tensão cai para 30   V . Sua resistência é 120   Ω quando acesa e infinitamente elevada quando apagada.

  1. Por quanto tempo a lâmpada se encontra ligada cada vez que o capacitor descarrega?
  2. Qual é o intervalo de tempo entre acendimentos da lâmpada?

Passo 1

Beleza gente, vamo pra cima! A luz está ligada de 75   V o l t s até 30   V o l t s . Durante esse tempo a gente tem essencialmente um resistor de 120   Ω em pararelo com um capacitor de 6   μ F .

v 0 = 75   V ,     v ∞ = 0   V ,     τ = 120 × 6 × 10 - 6 = 0.72   m s

v t 1 = 74 e - t 1 / τ = 30 , o que leva a t 1 = - 0.72 ln ⁡ 0.4 m s = 659.7   μ s

Passo 2

Para acharmos o intervalo de tempo, vamos jogar na formula!

τ = R C = 4 × 10 6 6 × 10 - 6 = 24   s

Desde,

v t = v ∞ + v 0 - v ∞ e - t / τ

v t 1 = v ∞ + v 0 - v ∞ e - t 1 / τ

v t 2 = v ∞ + v 0 - v ∞ e - t 2 / τ

Dividindo a equação de t 1 e t 2 , temos que:

v t 1 - v ( ∞ ) v t 2 - v ( ∞ ) = e ( t 2 - t 1 ) / τ

t 0 = t 2 - t 1 = τ ln ⁡ v t 1 - v ∞ v t 2 - v ∞

t 0 = 24 ln ⁡ 75 - 120 30 - 120 = 24 ln ⁡ 2 = 16.636   s

Resposta

a ) 659.7   μ s  

b ) 16.636   s  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

8.37) Calcule v, se vg = 2e-3tu(t) V.
8.13) (a) Calcule v para t0, se o circuito está em regime permanente em t = 0-. (b) Repita a parte (a) se um resistor R1 é colocado em série com a fonte V0.
Calcule v 1 e v 2 para t0 , se o circuito está em regime permanente em t = 0 - .
8.39) Calcule v para t0, se vg = 3u(t) V.
A chave do circuito mostrado na Figura P7.61 esteve na posição OFF por um longo tempo. Em t=0, ela passa instantaneamente para a posição ON. Determine v 0 tp a r at ≥ 0 .