Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 9.Problemas - Ex. 29

Calcule i , t > 0 , se v (0) = 6 V e i (0) = 2 A

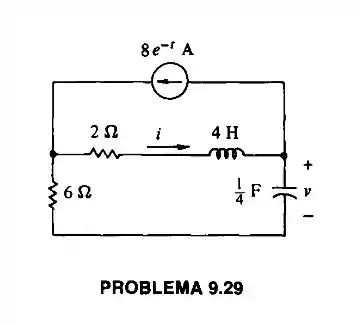
Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

Primeiro, vamos anotar algumas informações

i_1 = 8 e^(- t)

E

i = i_1 + i_2 = 8 e^(- t) + i_2

Nós queremos de i_2 , então

i_2 = i - 8 e^(- t)

Agora vamos fazer o equacionamento, com isso, nós temos que

0 = v + 6 i_2 + 2 i + 4 (d i)/(d t)

Desenvolvendo um pouco mais os termos, nós temos que

4 int i_2 d t + 6 (i - 8 e^(- t)) + 2 i + 4 (d i)/(d t) = 0

Um pouco mais...

4 i_2 + 6 (d i)/(d t) + 48 e^(- t) + 2 (d i)/(d t) + 4 (d^2 i)/(d t^2) = 0 -> 4 (d^2 i)/(d t^2) + 8 (d i)/(d t) + 4 i_2 = - 48 e^(- t)

Simplificando as coisas, nós temos que

(d^2 i)/(d t^2) + 2 (d i)/(d t) + i = - 4 e^(- t)

Passo 2

Chegamos na EDO, ok, agora temos que encontrar as raízes do polinômio característico, com isso, vamos supor que i seja uma função do tipo

i (t) = (A + B t) e^(- t)

E temos uma corrente “final” demarcada pela função

i_F (t) = C t^2 * e^(- t)

Consequentemente, a primeira derivada é igual a

i_F^' (t) = 2 C t * e^(- t) - C t^2 e^(- t)

E a segunda derivada...

i_F^(' ') (t) = 2 C e^(- t) - 2 C t e^(- t) - 2 C t e^(- t) + C t^2 e^(- t) = 2 C e^(- t) - 4 C t e^(- t) + C t^2 e^(- t)

Agora, vamos voltar para a EDO,

[2 C e^(- t) - 4 C t e^(- t) + C t^2 e^(- t)] + 2 [2 C t * e^(- t) - C t^2 e^(- t)] + [C t^2 e^(- t)] = - 4 e^(- t)

Isso tudo se resume em

2 C = - 4

Logo

C = - 2

Agora voltando para a função e descobrindo os outros termos, nós temos a seguinte relação

i_F (t) = - 2 t^2 e^(- t) A

No instante 0, temos que

i (0) = 2 -> A = 2

Passo 3

Vamos pegar a derivada agora, para encontrar o B, com isso nós temos que

(d i)/(d t) = (V)/(L) -> (d i)/(d t)_t = 0 = (6)/(4) = (3)/(2)

Com isso, nós obtemos a seguinte configuração

(3)/(2) = B e^(- t) - (A + B t) e^(- t)

No instante 0

(3)/(2) = B - A -> B = (3)/(2) + A

Como A = 2 , portanto, nós temos que

B = (3)/(2) + 2 = (7)/(2)

Logo, a expressão da corrente é igual a

i (t) = (2 + (7)/(2) t - 2 t^2) e^(- t) A

Resposta

i (t) = (2 + (7)/(2) t - 2 t^2) e^(- t) A

Exercícios de Livros Relacionados

Em um circuito RLC, fazer R = 0 produzirá:(a) resposta com amortecimento supercrítico(b) resposta com amortecimento crítico(c) resposta com subamortecimento(d) resposta com não amortecimento(e) nenhum
Quando uma entrada em degrau é aplicada a um circuito de segunda ordem, os valores finais das variáveis de circuito são encontrados:(a) substituindo os capacitores por circuitos fechados e os indutore
Considere o circuito RLC em paralelo da Figura 8.60. Que tipo de resposta ele produzirá?(a) com amortecimento supercrítico(b) com subamortecimento(c) com amortecimento crítico(d) nenhuma das alternati
Um circuito RLC em paralelo possui L = 2 H e C = 0,25 F. O valor de R que produzirá um fator de amortecimento unitário é:(a) 0,5 Ω (b) 1 Ω (c) 2 Ω (d) 4 Ω
Consulte o circuito RLC na Figura 8.59. Que tipo de resposta ela produzirá?(a) com amortecimento supercrítico(b) com subamortecimento(c) com amortecimento crítico(d) nenhuma das alternativas anteriore