Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 14.10 - Ex. 1

Calcule V_2 // V_g , para o circuito mostrado abaixo.

Passo 1

Iae, meus queridos! Td certinho?? 😉

Essa questão pode ser um pouco trabalhosa, mas garanto que a ideia por trás é bem fácil.

Temos o seguinte circuito:

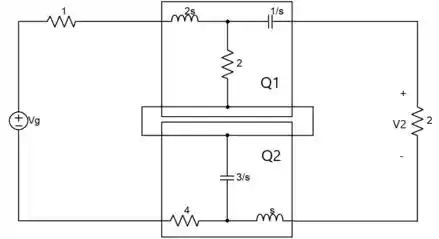
Vemos que se trata de uma associação sem série de quadripolos, sendo assim, vamos encontrar um quadripolo equivalente para o circuito.

Pra isso vamos calcular os parâmetros z de cada quadripolo e substituir nas equações de malhas.

{[[V_1 (s) = (Z_11 A + Z_11 B) I_1 (s) + (Z_12 A + Z_12 B) I_2 (s)],[V_2 (s) = (Z_2 1 A + Z_2 1 B) I_1 (s) + (Z_2 2 A + Z_2 2 B) I_2 (s)]])

Passo 2

Analisando o quadripolo Q 1 :

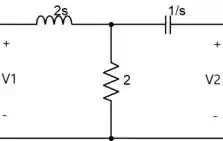
Escrevendo as equações das malhas V_1 e V_2 , podemos encontrar os parâmetros z.

{[[V_1 (s) = 2 s I_1 (s) + 2 (I_1 (s) + I_2 (s))],[V_2 (s) = (1)/(s) I_2 (s) + 2 (I_1 (s) + I_2 (s))]])

{[[V_1 (s) = ( 2 s + 2 ) I_1 (s) + 2 I_2 (s)],[V_2 (s) = 2 I_1 (s) + ((1)/(s) + 2) I_2 (s)]])

Vemos que os parâmetros z desse quadripolo, são:

Z_11 A = (2 s + 2)

Z_12 A = Z_21 A = 2

Z_22 A = ((1)/(s) + 2)

Passo 3

Analisando o quabripolo Q 2 :

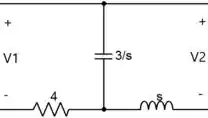
Escrevendo as equações das malhas V_1 e V_2 , podemos encontrar os parâmetros z.

{[[V_1 (s) = 4 I_1 (s) + (3)/(s) (I_1 (s) + I_2 (s))],[V_2 (s) = s I_2 (s) + (3)/(s) (I_1 (s) + I_2 (s))]])

{[[V_1 (s) = (4 + (3)/(s)) I_1 (s) + (3)/(s) I_2 (s)],[V_2 (s) = (3)/(s) I_1 (s) + (s + (3)/(s)) I_2 (s)]])

Vemos que os parâmetros z desse quadripolo, são:

Z_11 B = (4 + (3)/(s))

Z_12 B = Z_21 B = (3)/(s)

Z_22 B = (s + (3)/(s))

Passo 4

Calculando o quadripolo equivalente como descrito anteriormente...

{[[V_1 (s) = ((2 s + 2) + Z_11 B) I_1 (s) + (Z_12 A + Z_12 B) I_2 (s)],[V_2 (s) = (Z_21 A + Z_21 B) I_1 (s) + (Z_22 A + Z_22 B) I_2 (s)]])

{[[V_1 (s) = ((2 s + 2) + (4 + (3)/(s))) I_1 (s) + (2 + (3)/(s)) I_2 (s)],[V_2 (s) = (2 + (3)/(s)) I_1 (s) + (((1)/(s) + 2) + (s + (3)/(s))) I_2 (s)]])

Organizando tudo, temos:

Z_11 e q = 2 s + 2 + 4 + (3)/(s) -> Z_11 e q = (2 s^2 + 6 s + 3)/(s)

Z_12 e q = Z_21 e q = 2 + (3)/(s) -> Z_12 e q = Z_21 e q = (2 s + 3)/(s)

Z_22 e q = (1)/(s) + 2 + s + (3)/(s) -> Z_22 e q = (s^2 + 2 s + 4)/(s)

Passo 5

Para calcular o ganho V_2 // V_g , podemos utilizar a equação 14.57.

(V_2)/(V_g) = (Z_21 e q Z_L)/((Z_11 e q + Z_g) (Z_22 e q + Z_L) - Z_12 e q Z_21 e q)

Onde Z_L = 2 e Z_g = 1 , substituindo os valores que encontramos anteriormente nesta equação, temos...

(V_2)/(V_g) = (((2 s + 3)/(s)) 2)/((((2 s^2 + 6 s + 3)/(s)) + 1) ((s^2 + 2 s + 4)/(s) + 2) - ((2 s + 3)/(s)) ((2 s + 3)/(s)))

(V_2)/(V_g) = ((4 s + 6)/(s))/(((2 s^2 + 6 s + 3)/(s) + (1 s)/(s)) ((s^2 + 2 s + 4)/(s) + (2 s)/(s)) - ((2 s + 3)/(s)) ((2 s + 3)/(s)))

(V_2)/(V_g) = ((4 s + 6)/(s))/(((2 s^2 + 7 s + 3)/(s)) ((s^2 + 4 s + 4)/(s)) - ((4 s^2 + 12 s + 9)/(s ²)))

Vamos multiplicar o numerador e o denominador por s no numerador da equação para facilitar nossos cálculos.

(V_2)/(V_g) = ((4 s^2 + 6 s)/(s^2))/(((2 s^2 + 7 s + 3)/(s)) ((s^2 + 4 s + 4)/(s)) - ((4 s^2 + 12 s + 9)/(s ²)))

Observe que:

((2 s^2 + 7 s + 3)/(s)) ((s^2 + 4 s + 4)/(s)) = (2 s^2 + 7 s + 3) (s^2 + 4 s + 4) ((1)/(s^2))

Logo...

(V_2)/(V_g) = ((4 s^2 + 6 s) ((1)/(s^2)))/((2 s^2 + 7 s + 3) (s^2 + 4 s + 4) ((1)/(s^2)) - (4 s^2 + 12 s + 9) ((1)/(s^2)))

(V_2)/(V_g) = ((4 s^2 + 6 s))/((2 s^2 + 7 s + 3) (s^2 + 4 s + 4) - (4 s^2 + 12 s + 9))

(V_2)/(V_g) = (4 s^2 + 6 s)/(2 s^4 + 15 s^3 + 35 s^2 + 28 s + 3)

Foi tranquilo? Bora pra mais uma! 😎

Resposta

(V_2)/(V_g) = (4 s^2 + 6 s)/(2 s^4 + 15 s^3 + 35 s^2 + 28 s + 3)

Exercícios de Livros Relacionados

10.30. Calcule a tensão v em regime permanente, se Vg = 5 cos 2t V..
10.31. Calcule o valor de v em regime permanente.
10.32. Calcule os valores v e v1 em regime permanente.
Desenhe o diagrama de polos e zeros da função de rede do Ex. 14.5.1
Se a equação representativa de um circuito é d 2 v o d t 2 + 4 ⋅ d v o d t + 13 v o = 2 ⋅ d v i d t + 4 v i Calcule H(s) e os polos e zeros.