Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.Problemas - Ex. 18
Calcule para , se o circuito está em regime permanente em
Passo 1
Iae, meus queridos! Td certinho?
Mais uma questão daquelas pra relaxar de tão tranquila que é.
A questão nos disse que o circuito está em regime permanente no instante , portanto o circuito terá essa cara quando .
Esse circuito vai nos servir para calcularmos .
Como o circuito está em regime permanente em , podemos considerar o indutor como um fio ideal, dessa forma basta aplicarmos o método de divisão de correntes para encontrar .
Passo 2
Já quando , o circuito terá essa cara:
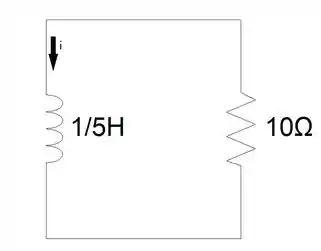
Por fim, basta substituirmos os valores que temos na equação geral da descarga de um indutor.
Viu só, falei que ia ser tranquilinha. Deu nem pra cansar, bora pra outra!
Resposta
Exercícios de Livros Relacionados
A chave no circuito da Figura P7.15 esteve fechada por um longo tempo antes de abrir em t = 0. Determine a) i L(t), t $ 0. b) vL(t), t $ 0+. c) i Δ(t), t $ 0+.
As duas chaves mostradas no circuito da Figura P7.17 funcionam simultaneamente. Antes de t = 0, cada chave estava na posição indicada por um longo tempo. Em t = 0, elas passam instantaneamente para su
No circuito mostrado na Figura P7.19, a chave esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente de a para b. a) Determine i o (t) para t $ 0. b) Qual é a energia total forne
A fonte de 240 V, e resistência interna de 2 V, no circuito da Figura P7.20, sofre inadvertidamente um curto-circuito em seus terminais a,b. No instante em que a falha ocorre, o circuito estava em fun
Segue o mesmo raciocínio da questão anterior, só que agora quer saber coisas relacionadas a energia armazenada.