Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 7.Problemas - Ex. 15

A chave no circuito da Figura P7.15 esteve fechada por um longo tempo antes de abrir em t = 0. Determine a) i L(t), t $ 0. b) vL(t), t $ 0+. c) i Δ(t), t $ 0+.

Passo 1

[a] – Para t

Logo, para i L ( 0 ) :

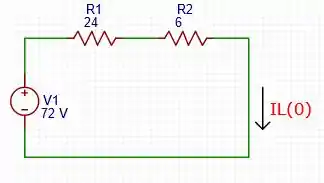
i L 0 = - 72 24 + 6 = - 2.4   A

No instante t > 0, tem-se uma fonte dependente, logo vamos usar Thévenin:

i Δ = - 100 160 i T =   - 5 8 i T

E com isso podemos encontrar v T :

v T = 20 i Δ + i T 100 60 160 =   - 12.5 i T + 37.5 i T

v T i T = R T h = - 12.5 + 37.5 = 25   Ω

Logo, o circuito RL fica da seguinte forma:

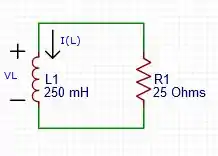
Agora, podemos calcular a constante de tempo:

τ = L R = 250 × 10 - 3 25 → 1 τ = 100

A equação da corrente do indutor:

i L = - 2.4 e - 100 t   A ,     t ≥ 0

Passo 2

[b] - A equação da tensão é igual a:

v L = 250 × 10 - 3 240 e - 100 t = 60 e - 100 t   V ,     t ≥ 0 +

Passo 3

[c] - E a corrente de delta é dada pela seguinte relação:

i   Δ = 0.625 i L = - 1.5 e - 100 t   A ,     t ≥ 0 +  

Resposta

a )   i L = - 2.4 e - 100 t   A ,     t ≥ 0

b )   v L =   60 e - 100 t   V ,       t ≥ 0 +  

c )   i   Δ = 0.625 i L = - 1.5 e - 100 t   A ,     t ≥ 0 +

Exercícios de Livros Relacionados

A chave do circuito mostrado na Figura P7.37 esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente para a posição b. a) Determine a expressão numérica para i o (t) quando t $ 0.
A corrente e a tensão nos terminais do indutor no circuito da Figura 7.16 são i(t) = (4 + 4e-40t ) A, t $ 0; v(t) = -80e-40t V, t $ 0+. a) Especifique os valores numéricos de Vs , R, Io e L. b) Em qua
a) Use os valores dos componentes do Apêndice H para criar um circuito RL de primeira ordem (veja a Figura 7.16) com uma constante de tempo de 8 ms. Use um único indutor e uma rede de resistores, se n
Repita o Problema 7.37, assumindo que a chave no circuito da Figura P7.37 esteve na posição b por um longo tempo e passa para a posição a em t = 0, onde permanece.
Um circuito RL em série tem um indutor de 1H . Determine o valor de R para que a energia armazenada se reduza à metade a cada 10m s .