Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.Problemas - Ex. 22
Calcule para , se o circuito está em regime permanente em .
Passo 1
Iae, meus queridos! Td blzinha?
Quando , o circuito tem a seguinte característica:
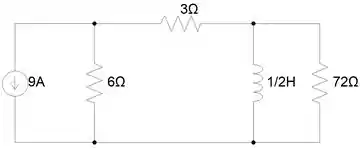
A questão nos diz que no instante , o circuito está em regime permanente. Isso significa que o indutor se comporta como um fio ideal nesse instante, portanto podemos desconsiderar o resistor de 72Ω por enquanto.
Nesse instante, a corrente que passa pelo resistor de 3Ω, será a mesma que passa pelo indutor, então temos que calcula-la pois será nosso valor , para isso, vamos utilizar o método de divisão de corrente.
Passo 2
Já quando , o circuito se comporta assim:
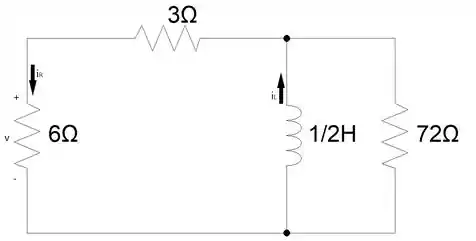
Nessa etapa, temos que calcular e aplicar a Lei de Ohm para encontrar . Antes vamos calcular o do circuito.
Com essas informações que obtemos, podemos formular a função .
Agora aplicamos o método de divisão de corrente.
Por fim, aplicando a Lei de Ohm no resistor de 6Ω.
Iae, foi tranquilo? Não pare agora não, bora pra mais uma!