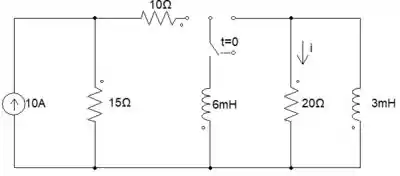
Calcule para , se o circuito está em regime permanente em
Passo 1
Fala, galerinha. Tudo certinho com vocês?

Já estão craques, tenho certeza disso. Mas, vamos continuar praticando. Olha só esse circuito RL que interessante, tem uma chave bem no meio dele! Massa né? Vamos meter bronca 💪
Para começar, vamos analisar o circuito em regime permanente, para isso temos que desconectar toda a parte depois da chave. Se liga como o circuito fica agora:
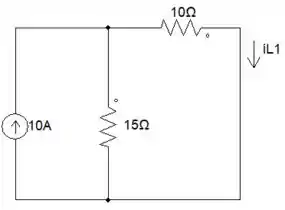
Show de bola! Essa parte vai ser bem tranquila. Temos um circuito simples com uma fonte de corrente e afim de descobrirmos o Esse modelo de circuito te lembra alguma coisa? Isso mesmo, divisão de corrente!
Passo 2
Rapaz...essa parte do regime permanente foi super fácil né? Será que no regime transitório também será assim? Vamos conferir 💪
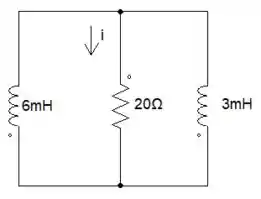
Olha só pessoal, ficamos com um resistor e dois indutores que estão em parelho, então precisamos fazer a associação desses indutores.
//
//
//
E, assim, fica o circuito equivalente
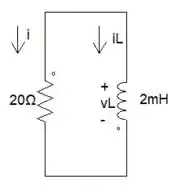
Passo 3
Está indo muito bem! Após termos achado o circuito equivalente, vamos fazer LKT na malha.
Massa! Achamos a EDO.
Passo 4
incrível, pessoal! Estamos no final!!! Agora, vamos definir um nó a que vai estar ligando o resistor de 20Ω e o indutor de 2mH, feito isso iremos fazer LKC nesse nó:
Muito bem! E quanto vale o ? Vamos usar a equação . Lembrando que nosso . Vamos lá!
Como , então:
E aí, o que achou dessa questão? Conta para a gente!
Até a próxima pessoal 👍