Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 13.Problemas - Ex. 27
Calcule as correntes de linha , e .
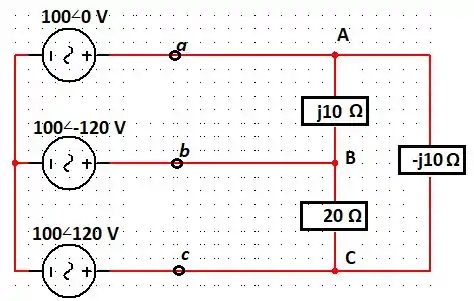
Passo 1
Eaee, seguinte... Vamos primeiro começar pela parte mais simples. De cara, podemos descobrir as correntes de fase da seguinte forma (lembrando que a relação entre a tensão de linha e a tensão de fase em é multiplicada por e defasada em ):
Passo 2
Agora, analise o seguinte circuito:
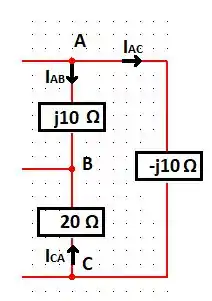
Pela Lei dos Nós, temos:
Faaacil né?? Responde aí!!!
Resposta
Exercícios de Livros Relacionados
Uma fonte equilibrada conectada em Y , c o m V a n = 2400 V (eficazes), de seqüência positiva, é conectada por quatro condutores perfeitos a uma carga desbalanceada conectada e m Y , Z A N = 10 Ω ,
Repita o Prob. 13.31 , se Z 1 = Z 2 = Z 3 = 10600 ∘ Ω . Note que, neste caso, o wattímetro C lê a potência total, pois o wattímetro A lê zero.
No sistema Y = Δ equilibrado, a carga consome 3k W , com fator de potência 0,8 atrasado. Capacitores sáo conectados a cada fase da carga, para aumentar seu fator de potência para 0,9 atrasado. Calcule
No sistema Y - A do Prob. 13.17, a tensão da fonte, V a n = 100 / 0 ∘ V (eficazes) e Z p = 10 / 60 ∘ Ω . Calcule a tensão de linha, a corrente de linha, os módulos da corrente da carga e a potência en
C a l c u l e a c o r r e n t e d e l i n a I_L