Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 14.Problemas - Ex. 9

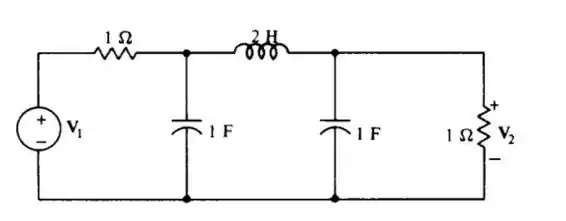
Use o princípio da proporcionalidade para calcular a função de rede V 2 V 1 e use o resultado para calcular a resposta forçada v 2 ( t ) , quando v 1 ( t ) = 4 c o s ⁡ t   V

Passo 1

Fala aí galera tudo certinho? O enunciado pede que a gente calcula a função de rede V 2 V 1 e use o resultado para calcular a resposta forçada v 2 ( t ) , quando v 1 ( t ) = 4 c o s ⁡ t   V .

y ' = s + 1

z e q ' = 2 s + 1 s + 1 = 2 s 2 + 2 s + 1 s + 1

y e q ' ' = s + 1 2 e q ' = s + s + 1 2 s 2 + 2 s + 1 = 2 s 3 + 2 s 2 + 2 s + 1 2 s 2 + 2 s + 1

V 1 = V 1 ⋅ 1 / y e q   ' ' 1 + 1 / y e q '

V 2 = V x ⋅ 1 / y ' Z e q ' =

V 2 = V 1 ⋅ 1 1 + y e q ' ' - 1 y ' Z e q '

Passo 2

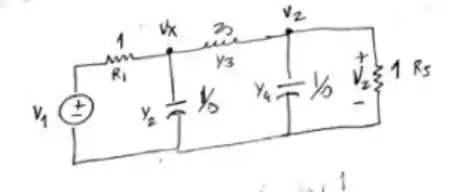
Para v 1 t = 4 c o s c o s   t               s = j                             v ( s ) = 4 ∠ 0

Y e q   ( j ) ' ' = 0,2 + 0,4 j

y ' Z e q ' = ( s + 1 ) ⋅ 2 s 2 + 3 s + 1 ( s + 1 ) = - 1 + 2 j

V 2 = 4 ⋅ 1 1 + 0,2 + 0,4 j ⋅ 1 - 1 + 2 j = - 1 - j = 2 < - 135 0

V 2 ( t ) = 2 c o s ⁡ t - 135 ∘ ⋅

Resposta

V 2 ( t ) = 2 c o s ⁡ t - 135 ∘ ⋅

Exercícios de Livros Relacionados

50- Determine v x no circuito da Figura 9.57 . Considere i s t = 5 cos ⁡ 100 t + 40 ° A
56- Com ω = 377r a d / s , determine a impedância de entrado do circuito mostrado na Figura 9.63 .
52- Se V o = 8 ∠ 30 °V no circuito da Figura 9.59 , determine I s .
57- Com ω = 1r a d / s , obtenha a impedância de entrada do circuito da Figura 9.64
55- Determine Z no circuito da Figura 9.62 dado que V o = 4 ∠ 0 °V