Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 14.8 - Ex. 1

Calcule os parâmetros z e os parâmetros ABCD do circuito mostrado na figura abaixo.

Passo 1

Iae, meus queridos! Td certinho??

Essa questão é bem tranquila, primeiro vamos calcular os parâmetros z:

Temos o circuito.

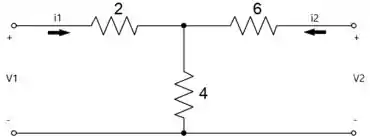
Vamos escrever as equações de V 1 s e V 2 s .

V 1 s = Z 11 I 1 s + Z 12 I 2 s V 2 s = Z 21 I 1 s + Z 22 I 2 s

Agora vamos escrever as equações da malha V 1 e V 2 .

V 1 s = 2 I 1 s + 4 ( I 1 s + I 2 s ) V 2 s = 6 I 2 s + 4 ( I 1 s + I 2 s )

V 1 s = 6 I 1 s + 4 I 2 s V 2 s = 4 I 1 s + 10 I 2 s

É isso! Por simetria, vemos todos os valores de z.

6 I 1 s + 4 I 2 s = Z 11 I 1 s + Z 12 I 2 s 4 I 1 s + 10 I 2 s = Z 21 I 1 s + Z 22 I 2 s

Logo...

Z 11 = 6 Ω

Z 12 = Z 21 = 4 Ω

Z 22 = 10 Ω

Passo 2

Por fim, vamos calcular os parâmetros ABCD, suas equações são.

V 1 s = A V 2 s - B I 2 s I 1 s = C V 2 s - D I 2 s

Vamos reutilizar as equações de malhas que usamos anteriormente.

V 1 s = 6 I 1 s + 4 I 2 s V 2 s = 4 I 1 s + 10 I 2 s

Vemos que o termo A é dado por:

A = V 1 s V 2 s ​ I 2 s = 0

Então vamos calcular a razão entre V 1 s e V 2 s

A = V 1 s V 2 s = 6 I 1 s + 4 I 2 s 4 I 1 s + 10 I 2 s ​ I 2 s = 0

A = V 1 s V 2 s = 6 I 1 s + 0 4 I 1 s + 0

A = V 1 s V 2 s = 6 4 → A = 3 2

Passo 3

O termo B é dado por:

B = - V 1 s I 2 s ​ V 2 s = 0

Igualando V 2 s = 0 nas equações das malhas e isolando I 1 s .

V 2 s = 4 I 1 s + 10 I 2 s = 0

4 I 1 s = - 10 I 2 s

I 1 s = - 10 I 2 s 4

Substituindo em V 1 s .

V 1 s = 6 I 1 s + 4 I 2 s

V 1 s = 6 - 10 I 2 s 4 + 4 I 2 s

V 1 s = - 60 I 2 s 4 + 16 I 2 s 4

V 1 s = - 44 I 2 s 4

- B = V 1 s I 2 s = - 11

B = 11

Passo 4

O termo C é dado por:

C = I 1 s V 2 s ​ I 2 s = 0

Manipulando a equação da malha V 2 , temos.

V 2 s = 4 I 1 s + 10 I 2 s

V 2 s = 4 I 1 s + 0

V 2 s I 1 s = 4

C = I 1 s V 2 s = 1 4

C = 1 4

Passo 5

Por fim, o temo D é dado por:

D = - I 1 s I 2 s ​ V 2 s = 0

Manipulando a equação da malha V 2 , temos.

V 2 s = 4 I 1 s + 10 I 2 s

0 = 4 I 1 s + 10 I 2 s

4 I 1 s = - 10 I 2 s

- D = I 1 s I 2 s = - 10 4 = - 5 2

D = 5 2

Tranquilo? Tenho ctz q vc tirou de letra!

Resposta

Z 11 = 6 Ω

Z 12 = Z 21 = 4 Ω

Z 22 = 10 Ω

A = 3 2

B = 11

C = 1 4

D = 5 2

Exercícios de Livros Relacionados

Mostre que, no Prob. 15.6, se L = Q , C = 1 / Q e R = 1 , então H s = 1 Q s s 2 + 1 Q s + 1 Que é uma função de rede passa-faixa com índice de mérito Q , frequência central ω 0 = 1 rad/s, largura de f
Para o circuito mostrado, R = 2 Ω , L = 2H e C = 0.02F . Se a entrada e a saída forem V 1 e V 2 , respectivamente, calcule a função de rede e esboce as respostas em amplitude e fase. Mostre que o pico
Escolha C = 0.1 μ F e calcule R e L no Prob. 15.6, de forma que ω 0 = 10 4 rad/s e B = 10 4 rad/s.
10.22. Calcule a reatância X tal que a impedância vista pela fonte seja real. Para este caso, calcule a corrente em regime permanente i(t) correspondente a I se w = 10 rad/s.
10.25. Calcule a corrente i em regime permanente.