Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 2.5 - Ex. 4

Calcule v e a potência entregue pela fonte.

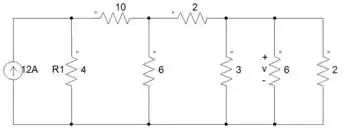
Passo 1

A questão pede a tensão no resistor de 24Ω e potência entregue pela fonte de 12A. Então, vamos lá!

Primeiro, vamos descobrir o R e q desse circuito, fazendo a associação dos resistores.

O resistor de 2Ω está em paralelo com de 6Ω:

R_2 \\ \\ 6 = (2 * 6)/(2 + 6)

R_2 \\ \\ 6 = (12)/(8)

R_2 \\ \\ 6 = 2,5 Ω

O resistor de 1,5Ω está em paralelo com de 3Ω:

R_1,5 \\ \\ 3 = (1,5 * 3)/(1,5 + 3)

R_1,5 \\ \\ 3 = (4,5)/(4,5)

R_1,5 \\ \\ 3 = 1 Ω

O resistor de 1Ω está em série com o de 2Ω:

R_1 - 2 = 1 + 2

R_1 - 2 = 2 Ω

O resistor de 3Ω está em paralelo com de 6Ω:

R_3 \\ \\ 6 = (3 * 6)/(3 + 6)

R_3 \\ \\ 6 = (18)/(9)

R_3 \\ \\ 6 = 2 Ω

O resistor de 2Ω está em série com o de 10Ω:

R_2 - 10 = 2 + 10

R_2 - 10 = 12 Ω

O resistor de 12Ω está em paralelo com de 4Ω:

R_12 \\ \\ 4 = (12 * 4)/(12 + 4)

R_12 \\ \\ 4 = (48)/(16)

R_12 \\ \\ 4 = 3 Ω

Este é o nosso circuito equivalente:

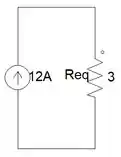
Passo 2

Agora que sabemos o circuito equivalente, podemos descobrir o V e q . Relaxa! É bem facinho, só vamos usar a lei de Ohm.

V e q = R e q * i

V e q = 3 * 12

V e q = 36 V

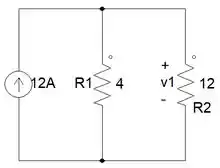
Agora está mais perto de descobrirmos o valor de v . Mas, antes temos que saber a tensão que está passando pelo resistor de 12Ω. Vamos chamar essa tensão de v 1 .

Para descobrir o v 1 vamos usar divisor de tensão.

v 1 = (R 1 * V e q)/(R 1 + R 2)

v 1 = (4 * 36)/(4 + 12)

v 1 = (144)/(16)

v 1 = 9 V

Já descobrimos o v 1 , vamos achar agora o v 2 e o v 3 .

Podemos ver na figura abaixa onde está o v 2 . Vamos fazer divisor de tensão mais uma vez para achá-lo!

v 2 = (R 3 * v 1)/(R 3 + R 4)

v 2 = (3 * 9)/(6 + 3)

v 2 = (27)/(9)

v 2 = 3 V

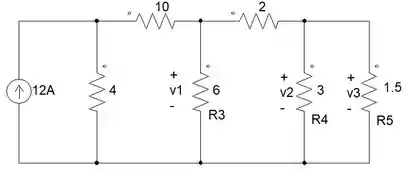
Como fizemos para achar o v 2 , vamos fazer para achar o v 3 .

v 3 = (R 4 * v 2)/(R 4 + R 5)

v 3 = (3 * 3)/(3 + 1,5)

v 3 = (9)/(4,5)

v 3 = 2 V

Agora sim vamos encontrar nosso v ‼ !

Vamos usar o v 3 na próxima divisão de tensão, que é a tensão que está passando na associação dos resistores R 6 e R 7 .

v = (R 7 * v 3)/(R 6 + R 7)

v = (2 * 2)/(6 + 2)

v = (8)/(8)

v = 1 V

Passo 3

Agora só falta descobrirmos qual a potência do nosso circuito. Fica tranquilo! É a parte mais rápida desse nosso problema! Só vamos utilizar a fórmula de potência que já conhecemos.

P = v e q * i

P = 36 * 12

P = 432 W

Resposta

v = 1 V

P = 432 W

Exercícios de Livros Relacionados

Uma tela touch resistiva tem 640 pixels na direção x e 1.024 pixels na direção y. A malha resistiva tem 8 V aplicados em ambos os sentidos, x e y. As coordenadas de pixel no ponto de toque são (480, 1
72 a) Usando a Figura 3.38, deduza a expressão para a tensão vy.b) Supondo que haja py pixels na direção y, deduza a expressão para a coordenada y do ponto de toque, usando o resultado de (a).
Suponha que a tela sensível ao toque descrita no Problema 3.74 é tocada simultaneamente em dois pontos, um com coordenadas (480, 192) e outro com coordenadas (240, 384). a) Calcule a tensão medida nas
Uma tela touch resistiva tem 5 V aplicada à malha na direção x e na direção y. A tela tem 480 pixels na direção x e 800 pixels na direção y. Quando a tela é tocada, a tensão na malha x é 1 V e a tensã
Use uma transformação D-Y para determinar as tensões v1 e v2 no circuito da Figura P3.59.