Use uma transformação D-Y para determinar as tensões v1 e v2 no circuito da Figura P3.59.
Passo 1
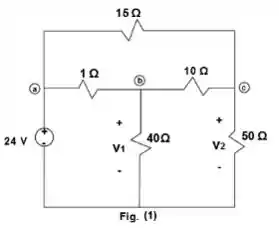
Transformando abc com transformação delta/estrela
, a resistência equivalente é de:
, a resistência equivalente é de:
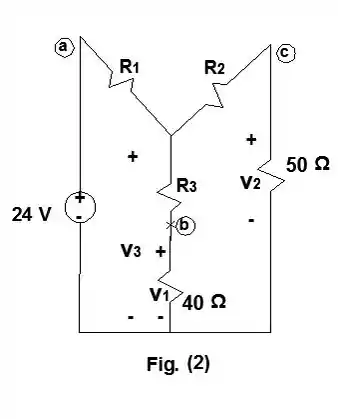
Passo 2
, q resistência equivalente é de:
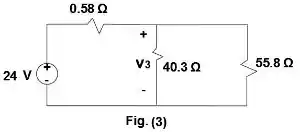
Usando divisor de tensão
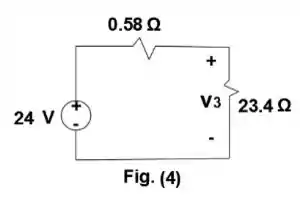
Da figura (2) e usando divisor de tensão