Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 9.Problemas - Ex. 36

Calcule o valor ou a faixa de valores de μ = 1 + R ≥ 1 tal que o circuito seja:

a) superamortecido;

b) subamortecido;

c) amortecimento crítico;

Passo 1

Fala aí pessoal tudo blz?

Nessa questão com base no circuito,

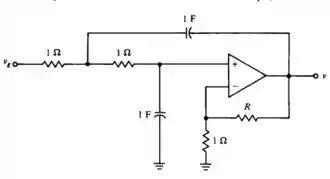
Devemos calcular o valor ou a faixa de valores de u = 1 + R ≥ 1 tal que,

a) superamortecido;

b) subamortecido;

c) amortecimento crítico;

Confia e vem comigo.

Passo 2

Na letra (a) sabendo que é superamortecido temos,

∆ > 0

y t = A e α t + B e α t

Ficando,

e - t + 2 e 2 t

Na letra (b) sabendo que é subamortecido, temos

∆ < 0

y t = A e α t cos ⁡ β t + B e α t sin ⁡ ( β t )

Ficando,

y t = 5 cos ⁡ ( 3 t ) + 6 sin ⁡ ( 3 t )

E por fim na letra ( c ) quando é criticamente amortecido temos,

∆ = 0

y t = A e α t + B t e α t

Ficando,

y t = - 9 + 4 t e 2 t + 4 t e 2 t

Espero ter ajudado, bons estudos e até a próxima.

Resposta

a) e - t + 2 e 2 t

b) y t = 5 cos ⁡ ( 3 t ) + 6 sin ⁡ ( 3 t )

c) y t = - 9 + 4 t e 2 t + 4 t e 2 t

Exercícios de Livros Relacionados

Calcule v 1 e v 2 para t0 , se o circuito está em regime permanente em t = 0 - .
8.39) Calcule v para t0, se vg = 3u(t) V.
A chave do circuito mostrado na Figura P7.61 esteve na posição OFF por um longo tempo. Em t=0, ela passa instantaneamente para a posição ON. Determine v 0 tp a r at ≥ 0 .
O capacitor do circuito visto na Figura P7.76 foi carregado até 300 V. Em t=0, a chave 1 fecha-se, fazendo com que o capacitor se descarregue na rede resistiva. A chave 2 fecha-se 200 μ s depois do fe