Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 7.Problemas - Ex. 61

A chave do circuito mostrado na Figura P7.61 esteve na posição OFF por um longo tempo. Em t=0, ela passa instantaneamente para a posição ON. Determine v 0 t   p a r a   t ≥ 0 .

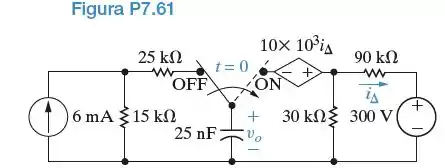
Passo 1

Falaaa, pessoal! Como vocês estão?

Bora pra mais uma questãozinha pra exercitar o que a gente sabe sobre resposta de circuitos RL e RC de primeira ordem!

Primeiramente, para t>0, com v 0 0 = 90 V , tem-se o seguinte iustrado:

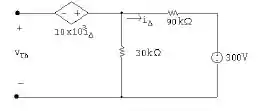
Colocando em números essa relação, temos que:

v T h = - 10   x   10 3 i ∆ + 30 120 300 = 100 V

Ou seja:

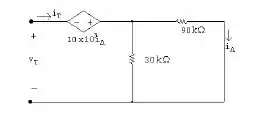
Colocando em números:

v T = - 10   x   10 3 i ∆ + 22,5   x   10 3 i T = 20   x   10 3   i T

R T h = v T i T = 20   k Ω

Passo 2

Por fim, para t>0:

v 0 = 100 + 90 - 100 e - t / T

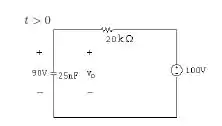
Mas sabemos que:

T = R C = 500   x   10 - 6

Logo:

v 0 = 100 - 10 e - 2000 t V

Resposta

v 0 = 100 - 10 e - 2000 t V

Exercícios de Livros Relacionados

A chave da figura 7.84 se encontra na posição A há um bom tempo. Suponha que a chave mude instantaneamente de A para B em t = 0 . Determine v para t0 .
No circuito mostrado na figura 7.81 v t = 56 ⋅ e - 200 tV ,t0 i t = 8 ⋅ e - 200 tm A ,t0 a Determine os valores de R e C ( b ) Calcule a constante de tempo τ c Determine o tempo necessário para a tens
No projeto de um circuito de comutação de sinais foi constatado que um capacitor de 100 mF era necessário para uma constante de tempo de 3 ms. Qual é o valor do resistor necessário para o circuito?
A chave na Figura 7.141 abre em t = 0. Use o PSpice ou MultiSim para determinar v(t) para t0.
Repita o Problema 7.49 usando o PSpice ou MultiSim.