Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.Problemas - Ex. 39

8.39) Calcule v para t > 0, se vg = 3u(t) V.

Passo 1

E aí galerinhaaa!! Vamos resolver essa questão juntinhos, beleza??

Nosso circuito é mostrado abaixo:

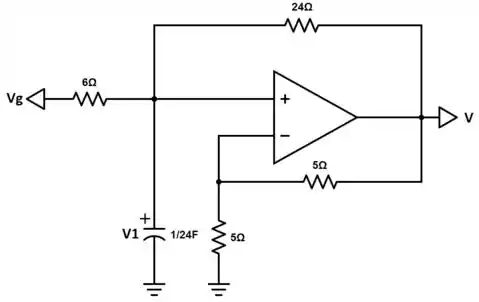
Primeiro, temos que v_g = 3 u ( t ) . Nesse caso, devemos analisar o circuito em dois momentos: t 0.

Para t

u (t) = 0 => v_g = 0 V

Como v_g é nulo e não consideramos nenhuma condição inicial para a energia armazenada no capacitor assume-se que esta é nula também. Portanto,

v (t) = 0 , t < 0

Para t > 0 temos:

u (t) = 1 => v_g = 3 V ( 1 )

Resposta ao degrau é dada na forma:

v = v_n + v_f ( 2 )

Vamos inicialmente determinar a resposta natural do sistema.

Levando em consideração que o amplificador é ideal, temos que as tensões nas entradas inversora e não-inversora devem ser iguais.

Começando a analisar o circuito pelo terminal positivo do Amp. Op. verificamos ao fazer LKC:

(v_g - v_1)/(6) + (v_n - v_1)/(2 4) - C (d v_1)/(d t) = 0 =>

4 v_g - 4 v_1 + v_n - v_1 - 24 C (d v_1)/(d t) = 0 =>

v_n = (d v_1)/(d t) + 5 v_1 - 4 v_g ( 3 )

Substituindo (1) em (3):

v_n = (d v_1)/(d t) + 5 v_1 - 12 ( 4 )

Analisando agora o terminal inversor do Amp. Op. temos:

v_n = 5 (v)/(10) + v_1 =>

v_n - (v)/(2) = v_1 => v_n = 2 v_1 ( 5 )

Substituindo (5) em (4):

(d v_1)/(d t) + 3 v_1 - 1 2 = 0 ( 6 )

Substituindo (d v_1)/(d t) por lambda em (6) temos:

lambda + 3 = 0 =>

lambda = - 3

Portanto, v_1 é dado na forma:

v_1 = A e^(lambda t) = A e^(- 3 t)

E v_n segundo (5) é dado na forma:

v_n = 2 A e^(- 3 t) => B e^(- 3 t) ( 7 )

Passo 2

Agora, precisamos analisar a resposta forçada do sistema.

Para isso, devemos nos lembrar que se trata de regime permanente e sendo assim, capacitor se comporta como um circuito aberto, logo v_1 = 0 .

Analisando as tensões nas entradas inversora e não-inversora percebemos que:

v_+ = v_- = (v_f)/(2) ( 8 )

Utilizando o resultado em (8) fazemos novamente LKC no terminal positivo do Amp. Op.:

(v_g - (v_f)/(2))/(6) + (v_f - (v_f)/(2))/(24) = 0 =>

4 (3 - (v_f)/(2)) + (v_f)/(2) = 0 =>

- 2 v_f + (v_f)/(2) = - 12 =>

(3 v_f)/(2) = 12 =>

v_f = 8 V ( 9 )

Combinando os resultados em (7) e (9) na equação (2):

v = B e^(- 3 t) + 8

Como sabemos que v (0) = v (0^-) = 0 então:

v (0) = B e^0 + 8 = 0 =>

B = - 8

Chegamos por fim:

v (t) = 8 (1 - e^(- 3 t)) V

Prontinhooo, essa teve muito cálculo, mas deu pra pegar a ideia, né? Bora pra mais uma??

Resposta

v (t) = 8 (1 - e^(- 3 t)) V

Exercícios de Livros Relacionados

A chave da figura 7.86 foi fechada há um bom tempo e é aberta em t = 0 . Determine v t para t ≥ 0 .
Determine a constante de tempo para o circuito da figura 7.83.
Para o circuito da figura 7.88, se v = 10 ⋅ e - 4 tVei = 0.2 ⋅ e - 4 t , t0 a Determine R e C . b Determine a constante de tempo. c Calcule a energia inicial no capacitor. d Obtenha o tempo necessário
A chave da figura 7.89 abre em t = 0 . Determine v_0 para t0 .
Para o circuito da figura 7.90, determine v 0 t para t0 . Determine o tempo necessário para a tensão no capacitor decair para um terço de seu valor em t = 0 .