Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 9.Problemas - Ex. 21

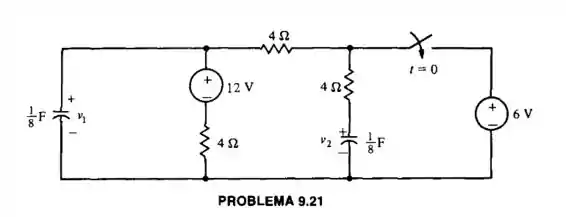
Calcule v 1 e v 2 para t > 0 , se o circuito está em regime permanente em t = 0 - .

Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

Vamos lá, para t < 0 o circuito está em regime permanente, logo os capacitores estão em aberto, com isso, a tensão no capacitor é uma constante, vamos olhar a expressão da corrente para o capacitor

i c t = C d v d t → i c t = 0

Como a corrente é zero, o capacitor será um circuito aberto em regime permanente, com isso, temos a seguinte configuração de circuito.

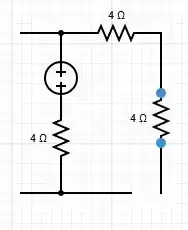
Como não circula corrente, a tensão será a mesma para os dois capacitores, e será a tensão da fonte, logo

v 1 0 = 12   V

v 2 0 = 12   V

Passo 2

Agora, vamos analisar depois de t ≥ 0 , temos que a LKT em v 1 é igual a

v 4 + C d v 1 d t + v 1 - 6 6 = 0  

Desenvolvendo os termos, nós temos que

1 8 d v 1 d t + 1 2 v 1 - 9 2 = 0 → d v 1 d t + 4 v 1 - 36 = 0

Logo,

d v 1 d t = 36 - 4 v 1

Agora, vamos calcular essa EDO, primeiro, vamos integrar a expressão

∫ 12 v 1   d v 1 36 - 4 v 1 = ∫ 0 t d t

Usando o método de substituição, temos a seguinte “nova” integral (só para facilitar nossos cálculos)

u = 36 - 4 v 1

d u =   - 4 d v 1

Com isso

- 1 4 ∫ d u u = t

A integral da esquerda nos fornece um logaritmo neperiano

- 1 4 ln ⁡ u = t →   - 1 4 ln ⁡ + 36 - 4 v 1 12 v 1 = t

Desenvolvendo um pouco mais,

- 1 4 ln ⁡ 36 - 4 v 1 - ln ⁡ 36 - 48 = t →   - 1 4 ln ⁡ 36 - 4 v 1   - 12 = t

Elevando a potência em relação ao logaritmo, nós temos que

ln ⁡ 36 - 4 v 1   - 12 1 / 4 = - t

Aplicando a exponencial,

e - t =   - 3 + 1 3 v 1 4 → e - 4 t = - 3 + 1 3 v 1

Logo, v 1 será igual a

v 1 3 =   - 3 + e - 4 t → v 1 = 9 + 3 e - 4 t   V

Passo 3

Para v 2 , nós temos que

6 = 4 i + v 2

Desenvolvendo um pouco mais, nós temos que

6 = 4 ∙ 1 8 d d t 6 - v 2 + v 2 → 6 =   - 1 2 d v 2 d t + v 2    

Com isso, nós temos que

1 2 d v 2 d t = v 2 - 6 → d v 2 2 v 2 - 12 = d t

Fazendo a integral dessa EDO, nós obtemos o seguinte resultado

∫ 12 v 2 d v 2 2 v 2 - 12 = ∫ 0 t d t

Mesmo sistema de substituição, então nós temos que

t = 1 2 ∫ d u u → 1 2 ln ⁡ u = 1 2 ln ⁡ ( 2 v 2 - 12 ) 12 v 2

Desenvolvendo os termos,

t = 1 2 ln ⁡ 2 v 2 - 12 - ln ⁡ 12 → 2 t = ln ⁡ 2 v 2 - 12 12

Aplicando a exponencial, nós temos que

e 2 t =   2 v 2 - 12 12 → 12 e 2 t = 2 v 2 - 12  

Logo

v 2 = 6 + 6 e 2 t   V

Resposta

v 1 = 9 + 3 e - 4 t   V

v 2 = 6 + 6 e 2 t   V

Exercícios de Livros Relacionados

Um circuito R C possui R = 2 Ω e C = 4F . A constante de tempo é: a0,5s b2s c4s d8s e15s
Um capacitor em um circuito R C com R = 2 Ω e C = 4F está sendo carregado. O tempo necessário para a tensão no capacitor atingir 63,2 % de seu valor em regime estacionário é: a2s b4s c8s d16s en e n h
Determine a constante de tempo para o circuito R C da figura 7.82.
Supondo que a chave na figura 7.87 se encontra na posição A há um longo período e seja mudada para a posição B em t = 0 . Em seguida, tem t = 1s , a chave se move de B para C . Determine v c t para t
Usando a figura 7.85, elabore um problema para ajudar outros estudantes a entenderem melhor os circuitos R C sem fontes.