Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 16.Problemas - Ex. 9
Calcule o valor de em regime permanente.
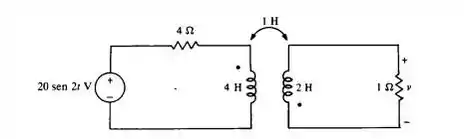
Passo 1
Vimos como circuitos com capacitores e indutores se comportam em duas situações particulares. A primeira delas pode ser chamada de instante inicial, geralmente associado a alguma alteração em um circuito em estado previamente conhecido, como por exemplo uma chave que estava fechada por muito tempo e é subitamente aberta. A segunda nós chamamos de regime permanente (ou regime estacionário
(1)
(2)
Da (2)
Sub-into (1)
Resposta
Exercícios de Livros Relacionados
Calcule o coeficiente de acoplamento k , se L_1 = 0,02 H , L_2 = 0.125 H e M = 0.01 H .
Repita o Prob, 16.13 , se omega = 4 r a d // s e t = pi // 8 s .
Calcule a corrente em regime permanente i 1 no Prob. 16.12 , usando a impedância refletida
Calcule a função de rede, H ( s ) = V_2 ( s ) // V_1 ( s ) . çã
Calcule i para t0 , se i ( 0 ) = 0 e v ( 0 ) = 4 V .