Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 7.Problemas - Ex. 35

Depois de a chave no circuito da Figura P7.35 estar aberta por um longo tempo, ela é fechada em t = 0. Calcule

(a) o valor inicial de i;

(b) o valor final de i;

(c) a constante de tempo para t ≥ 0 .

(d) a expressão numérica para i(t) quando t ≥ 0 .

Passo 1

[a] – Para t < 0 , calculando o equivalente de Thévenin para o circuito, temos:

Lembre-se que as fontes de tensão estão de uma forma em que podem ser configuradas assim, já que existem resistivos e indutivos no meio, com isso, podemos calcular a corrente em i ( 0 - ) .

i 0 - = 30 - 250 25000 + 30000 =   - 4   m A

Como o indutor não pode variar a corrente de forma instantânea, temos a seguinte relação matemática:

i 0 - = i 0 = i 0 +

Logo, temos:

i 0 - = i 0 + =   - 4   m A

Passo 2

[b] – Para t > 0   , a chave muda e com isso o circuito fica reduzido, dessa forma:

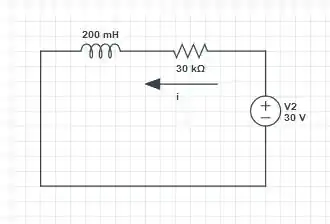
Quando i   t → ∞ o indutor se comporta um curto, então i vai ser:

i ∞ = 30 30000 = 1   m A

Passo 3

[c] – Agora fica mais simples, a constante de tempo é só jogar na fórmula:

τ = L e q R e q = 200 × 10 - 3 30000 = 6,67   μ s

Passo 4

[d] – Vamos usar a equação geral da corrente, essa aqui ( i t = I f + I 0 - I f e - t - t 0 τ )

i t = i ∞ + i 0 + - i ∞ e - t / τ

Substituindo os valores, temos:

i t = 0,001 + - 0,004 - 0,001 e - 150000 t

Convertendo para m A , se tem:

i t = 1 - 5 e - 150000 t   m A ,     t ≥ 0

Resposta

a )   i 0 - = i 0 + =   - 4   m A

b )     i ∞ = 4   m A

c )   τ = 6,67   μ s

d )   i t = 1 - 5 e - 150000 t   m A ,     t ≥ 0

Exercícios de Livros Relacionados

O pulso na figura 7.116a pode ser expressa em termos de funções de singularidade como: a2 u t + 2 u t - 1V b2 u t - 2 u t - 1V c2 u t - 4 u t - 1V d2 u t + 4 u t - 1V
Se v s mudar de 2 V para 4 V em t = 0 , podemos expressar v s como: aδ tV b2 u tV c2 u - t + 4 u tV d2 + 2 u tV e4 u t - 2V
No circuito da figura 7.80, i ∞ é: a10 A b 6 A c4 A d2 A e0 A
A fonte de corrente no circuito da Figura P7.81 (a) gera o pulso de corrente mostrado na Figura P7.81(b). Não há nenhuma energia armazenada em t=0.Deduza as expressões numéricas de v 0 ( t ) para os i
Calcule i para t0 , se v g = 12 u t V ,