Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 7.Problemas - Ex. 75

A chave do circuito mostrado na Figura P7.75 esteve na posição a por um longo tempo. Em t=0, ela passa para a posição b, onde permanece por 1 ms. Então, ela passa para a posição c, onde permanece indefinidamente. Determine

  1. i ( 0 + ) .
  2. i ( 200   μ s ) .
  3. i 6   m s .
  4. v ( 1 -   m s ) .
  5. v ( 1 +   m s ) .

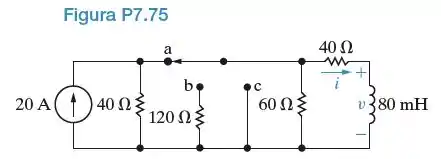
Passo 1

Falaaa, pessoal! Como vocês estão?

Bora pra mais uma questãozinha pra exercitar o que a gente sabe sobre resposta de circuitos RL e RC de primeira ordem!

  1. Para o primeiro intervalo, temos que:

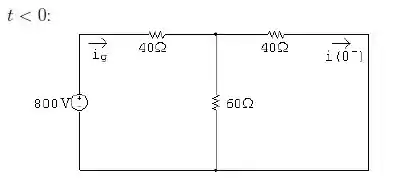
    2. Usando a Lei de Ohm’s, temos que:

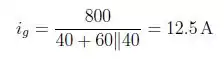
    O que nos leva a:

  2. Para o segundo intervalo temos que:

    3. Podemos encontrar o valor da frequência da seguinte forma:

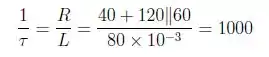
    Logo, podemos concluir que:

    Passo 2

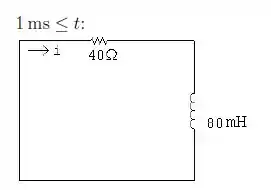
  3. Dessa vez, pra esse intervalo temos que:

    4. Para o período:

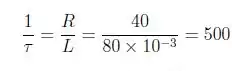
    Concluindo, temos:

  4. Para esse intervalo, temos que:

  5. Nesse item, temos o seguinte intervalo:

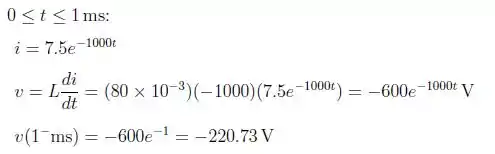
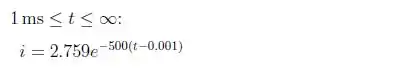
O que nos leva a:

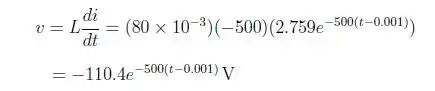
Concluindo

Resposta

Exercícios de Livros Relacionados

Depois de a chave no circuito da Figura P7.35 estar aberta por um longo tempo, ela é fechada em t = 0. Calcule (a) o valor inicial de i; (b) o valor final de i; (c) a constante de tempo para t ≥ 0 . (
A chave do circuito mostrado na Figura P7.36 esteve na posição a por um longo tempo antes de passar para a posição b em t = 0. a) Determine as expressões numéricas para i L(t) e vo (t) quando t $ 0. b
A chave do circuito mostrado na Figura P7.37 esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente para a posição b. a) Determine a expressão numérica para i o (t) quando t $ 0.
A corrente e a tensão nos terminais do indutor no circuito da Figura 7.16 são i(t) = (4 + 4e-40t ) A, t $ 0; v(t) = -80e-40t V, t $ 0+. a) Especifique os valores numéricos de Vs , R, Io e L. b) Em qua
a) Use os valores dos componentes do Apêndice H para criar um circuito RL de primeira ordem (veja a Figura 7.16) com uma constante de tempo de 8 ms. Use um único indutor e uma rede de resistores, se n