A chave da Figura é aberta em após o circuito ter atingido o estado estável. Determine e de modo que e .
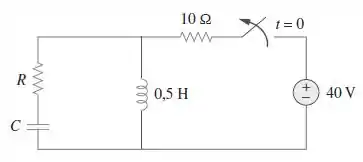
Passo 1
Vamos lá, pessoal! Se já nos foram dados os parâmetros e , podemos encontrar os valores de e a partir das seguintes equações:
Quando , passamos a ter um circuito RLC série, sem nenhuma fonte. Sabemos, então que o valor da indutância nesse circuito é igual a . Portanto, utilizando a equação de , podemos encontrar o valor de !
Passo 2
Por fim, precisamos achar o valor para , pois a partir dele podemos encontrar o valor de . Assim, temos:
Sabemos que . Logo,
Resposta
Os valores para e são: