Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 7.7 - Ex. 2
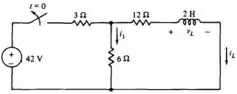
Se o circuito está em estado permanente cc em t = 0-, calcule (a) i1 (b) il e (c) vL em t = 0- e em t = 0+
Passo 1
Falaa galerinhaa!!! Tudo tranquilo?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para encontrar algumas correntes e tensões nos momentos em que a chave está aberta e fechada. Puts!! Já parece difícil?? Vai ser tranquilo. Partiu??
Passo 2
Ok, agora o nosso problema vai ser relembrar que quando o circuito está em regime permanente, o indutor se comporta como um curto-circuito, então suas tensões são iguais a zero. Responde Aí!! Lembrou?? Não?!
Bora resolver isso
Em , a chave está fechada, então o circuito ficará assim
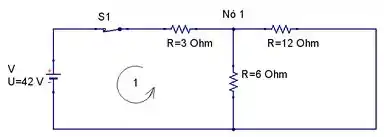
Pela LKT na malha externa, temos que
Pela LKT na malha 1, temos que
Pela LKC no nó 1, sabemos que
Assim, substituindo (3) nas equações (1) e (2), temos
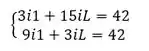
Resultando em
e
Como o indutor se comporta como um curto-circuito
Passo 3
Em , a chave está aberta, então o circuito ficará assim
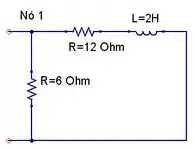
O indutor não permite a variação brusca de corrente, logo
Pela LKT no nó 1, temos que
Logo
Para finalizar, pela LKT, temos que
Tranquilo essa hein!!
Resposta
Em , , e
Em , , e