Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 6
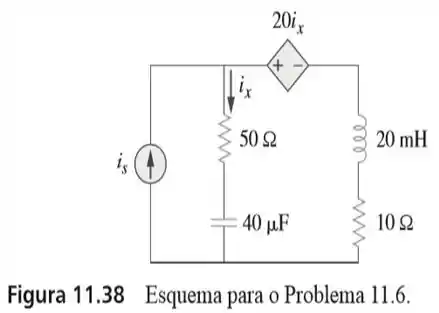
6. Para o circuito da figura , . Determine a potência média absorvida pelo resistor de .
Passo 1
E aí galerinha! Bora pra mais um probleminha sobre análise em circuitos de corrente alternada .
Bom! A primeira coisa que a gente tem que fazer, é descobrir com qual frequência estamos trabalhando em nosso circuito...
E é isso que vamos fazer! Do enunciado, tiramos que a nossa fonte de corrente é de .
E como a frequência é o termo que acompanha o tempo , então...
Agora, a próxima coisa que temos de fazer é passar os elementos desse circuito pro domínio da frequência...
Para fazer isso, basta usar as fórmulas abaixo...
Onde substituindo assim, os valores numéricos, obtemos as seguintes transformações...
Passo 2
E com os novos valores que temos, bora redesenhar o nosso circuito, já com todos os elementos no domínio da frequência.
O circuito vai ficar desse jeitinho aqui...
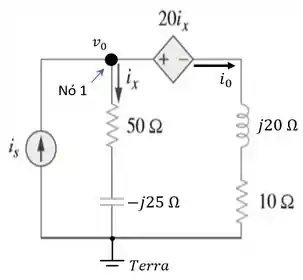
Pra não perder tempo, também já deixamos o circuito preparado pra fazer a análise nodal.
Esse nosso circuito tem dois nós, o nó do (que é padrão) e outro que chamamos de .
Vamos então, aplicar a lei das correntes de para o . Desse jeito...
E depois, colocar as correntes em função das tensões nodais... No caso, só temos uma, que é o !
É importante lembrar que a corrente sempre se desloca do potencial mais elevado até o menos elevado. Se é maior do que a tensão no , então a corrente vai do até o . Captou a linha de raciocínio?
Sendo assim, seguindo esse procedimento, chegamos até as seguintes equações...
Onde, substituindo elas na equação que obtivemos através da lei de , chegamos à seguinte equação abaixo...
Mas ainda não tá bom! Temos uma equação em função de duas variáveis! Como vamos resolver isso?
Fácil, Ora bolas! Anteriormente, descobrimos que...
Desse modo, substituindo isso na equação anterior...
Chegamos até uma boa relação, com apenas uma variável! Mas isso ainda está longe de ser resolvido! Pra ficar mais fácil da gente trabalhar, bora voltar tudo pra forma polar. Do seguinte jeito abaixo...
E então; aquela equação de antes...
Vai ficar assim agora...
Resolvendo ela, obtemos que...
Por fim, é só voltar tudo de novo pra forma retangular. Aí fica belezinha de resolver...
Passo 3
A corrente que está circulando no ramos onde está o resistor de é a corrente ...
Logo, é o valor de que precisamos descobrir para achar a potência no resistor de !
Ora bolas! Isso aí tá no papo! Do , sabemos que...
E uma vez que já conhecemos o valor de , então basta substituir...
Passo 4
Tamo quase terminando! Pra encontrar a potência média absorvido por um resistor em circuito , geralmente usamos a seguinte fórmula abaixo...
Onde é a resistência (que já temos) e é a corrente em valor .
No caso, o que estamos precisando aqui, é o valor da corrente .
Pois muito bem! Para encontrar isso, basta dividir por . Do seguinte jeitinho abaixo....
Encontrado o valor das nossas variáveis. A potência absorvida pelo resistor de será então, de:
E voilà! Terminamos aqui!
Até a próxima!