Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 3

3. Uma carga é formada por um resistor de 60   Ω em paralelo com um capacitor de 90   m F . Se a carga for conectada a uma fonte de tensão v s t = 160 cos ⁡ 2000 t , determine a potência média liberada para a carga.

Passo 1

Bora começar desenhando o circuito pra ficar mais fácil de entender:

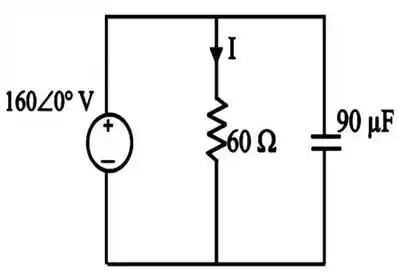
Passo 2

Agora, vamos calcular a corrente I usando a Primeira Lei de Ohm:

I = V R = 160 ∠ 0 ° 60   Ω = 2,666   A

Fizemos isso, porque para obter a corrente R M S , basta dividir o valor da corrente I por 2 :

I r m s = I 2

I r m s = 2,666   2   A

I r m s = 1,886   A

Passo 3

E pra calcular a potência média liberada, basta utilizar a fórmula abaixo:

P m e d = I r m s 2 R

Substituindo os valores numéricos pertinentes, obtemos que:

P m e d = ( 1,886   A ) 2 ⋅ ( 60   Ω )

P m e d = 213,33   W

Resposta

P m e d = 213,33   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

12.8. Calcule a potência média absorvida pelo resistor de 3·kΩ e pela fonte dependente.
12.7. Calcule a potência média absorvida pelos resistores e pela fonte.
Calcule o valor eficaz da tensão A - v = 8 + 6 2 cos ⁡ tV B – v = 4 cos ⁡ 3 t + 2 cos ⁡ 6 t + 12 cos ⁡ 8 t - 60 °V C - v = 4 cos ⁡ 2 t - 8 cos ⁡ 5 t + 6 2 cos ⁡ 3 t - 45 °V
Calcule a potência média entregue ao resistor de 4Ω .
Três cargas passivas paralelas, Z 1 , Z 2eZ 3 estão recebendo potências complexas de valores 3 - j 4 ,2 + j 5e3 + j 5V A , respectivamente. Se uma fonte de tensão de 20 ∠ 0 °V e f i c a z é conectada