Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 53

53- No circuito da Figura 11.72 , a carga A recebe 4   k V A com F P = 0.8 (adiantado). A carga B recebe 2.4   k V A com F P = 0.6 (atraso). C é uma carga indutiva que consome 1   k W e recebe 500   V A R .

( a ) Determine I

( b ) Calcule o fator de potência da associação.

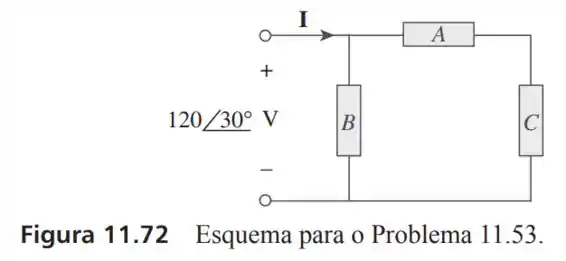
Passo 1

Vamos calcular a potência complexa em todas as cargas tal como fizemos na questão anterior:

S A = 4 × 0.8 - j 4 × 1 - 0.8 2   k V A = 3.2 - j 2 . 4 k V A

S B = 2.4 × 0.6 + j 2.4 × 1 - 0.6 2 = 1.44 + j 1.92 k V A

S C = 1 + j 0.5 k V A

Isso nos dá uma potência complexa igual a:

S = S 1 + S 2 + S 3 = 5.64 + j 0.02 k V A = 5.64 ∠ 0.2 °   k V A

Passo 2

Sabendo que a fonte de tensão está em R M S temos que a corrente total será:

S = V R M S I R M S *

I R M S * = S V R M S = 5.64   k V A ∠ 0.2 120 ∠ 30 = 47 ∠ - 29.8 °

Encontramos o conjugado da corrente, logo:

I R M S = 47   ∠ 29.8 °   A

Passo 3

Como temos o ângulo de 0.2   ° na potência total nós temos:

F P = cos ⁡ 0.2 = 0.999994

E como encontramos uma potência reativa positiva então a carga é indutiva, logo o fator de potência é atrasado.

Resposta

a )   I R M S = 47   ∠ 29.8 °   A

b )   F P = 0.999994   ( a t r a s a d o )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

43- Elabore um problema para ajudar outros estudantes a entender a potência complexa.
48- Determine a potência complexa para os seguintes casos: ( d ) V R M S = 220V ,P = 1k W,Z = 40Ω (indutivo)
48- Determine a potência complexa para os seguintes casos: ( c ) S = 600V A ,Q = 4 50V A R (indutivo)
46- Para os fasores de tensão e corrente a seguir, calcule a potência complexa, a potência aparente, a potência real e a potência reativa. Especifique se o F P está adiantado ou atrasado. c )V = 120∠
45- A tensão em uma carga e a corrente através dela são dadas por: v t = 20 + 60 cos ⁡ 100 tV i t = 1 - 0.5s e n100 tA Determine: ( a ) Os valores R M S de tensão e corrente ( b ) A potência média dis