Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 48d
48- Determine a potência complexa para os seguintes casos:
(indutivo)
Passo 1
Com os valores de e o módulo da impedância nós conseguimos encontrar a potência total, ou seja:
Passo 2
O que nos dá o seguinte triângulo de potências.
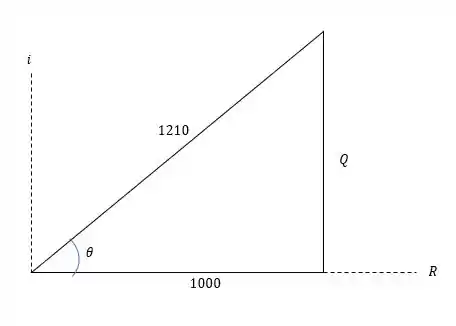
Então por Pitágora temos que o valor da potência reativa será:
E por ser positivo o valor de será positivo, nos dando então uma potência complexa igual a:
Resposta
Exercícios de Livros Relacionados
Para o circuito no domínio da frequência na Figura P10.51, calcule:a) o valor eficaz do módulo de V o ;b) a potência média dissipada no resistor de 160 V;c) a percentagem da potência média gerada pela
Suponhamos que uma impedância igual ao conjugado da impedância de Thévenin seja ligada aos terminais c,d do circuito mostrado na Figura P9.75.a) Determine a potência média fornecida pela fonte de tens
O transformador ideal ligado à carga de 5 kV no Problema 10.61 é substituído por um transformador ideal cuja razão entre espiras é 1:a.a) Qual é o valor de a para o máximo fornecimento de potência méd
As três cargas em paralelo no circuito da Figura P10.26 podem ser descritas da seguinte forma: a carga 1 está absorvendo uma potência média de 6 kW e fornecendo uma potência reativa de 8 kVARs; a carg
Suponha que a fábrica descrita no Problema 10.34 seja alimentada por uma linha cuja impedância é 0,25 + j0,1 V.A tensão na fábrica é mantida a 2.400 V (ef).a) Determine a perda de potência média na li