Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 55
Para o circuito da Figura , calcule a resistência equivalente.
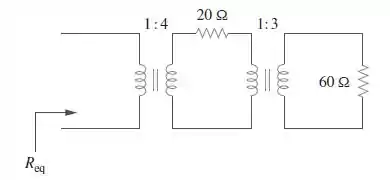
Passo 1
Galera, aqui temos dois transformadores ideais. A impedância de pode ser refletida ao primário:
Calculando a impedância total que agora está ligado ao secundário do primeiro transformador, temos:
Passo 2
Por fim, para obtermos a resistência equivalente, precisamos refletir a resistência para o primário do transformador. Assim,
Resposta
A resistência equivalente é igual a:
Exercícios de Livros Relacionados
Um transformador ideal de 440 / 110V pode ser conectado para se tornar um autotransformador ideal de 550 / 440V . Existem quatro ligações possíveis, duas das quais estão erradas. Determine a tensão de
Na Fig. 16.2(a), N 2 = 500 espiras e ϕ 21 = 200 μ W b , quando i 1 = 2A . Determine v 2 se i 1 = 10 c o s 100 tA .
Calcule a frequência para a qual a impedância refletida na figura 16.14 é real, se L 2 = 2HeZ 2 é um resistor 6Ω em série com um capacitor de 1 32 F
Dado: V g = 100 / 0 ° V , Z g = 40Ω ,L 1 = 0,5H ,L 2 = 0,1H ,M = 0,1Hew = 100 r a d s . Se Z 2 = 10 - j 1000 w Ω . Calcule:Se o ponto de polaridade estiver no terminal inferior do secundárioa) Z i n ;
Dado: V g = 100 / 0 ° V , Z g = 40Ω ,L 1 = 0,5H ,L 2 = 0,1H ,M = 0,1Hew = 100 r a d s . Se Z 2 = 10 - j 1000 w Ω . Calcule:a) Z i n ; b) I 1 ; c) I 2 ; d) V 1 ; e) V 2 .