Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 16.4 - Ex. 1
Dado:
/, Se Calcule:
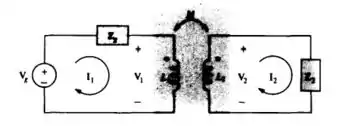
a)
b)
c)
d)
e)
Passo 1
Nessa questão dado:
/, Se Calcule:
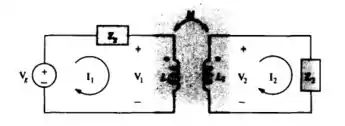
a)
b)
c)
d)
e)
Aposto que você tá com essa cara né? Hahaha fica tranquilo e vem.
Passo 2
Na letra (a) para temos,
Para,
Ficando,
Na letra (b) para
Ficando,
Passo 3
Na letra ( c ) para
Ficando,
Na letra (d) para achar
Ficando,
E por fim na letra (e) para
Ficando,
Espero ter ajudado, até próxima.
Resposta
a)
b)
c)
d)
e)
Exercícios de Livros Relacionados
36. Conforme feito na Figura 13.32 , obtenha as relações entre as tensões e correntes nos terminais para cada um dos transformadores ideais da Figura 13.105 .
39. Um transformador de 1.200 / 240VR M S tem impedância 60 ∠ - 30 °Ω no lado de alta tensão. Se o transformador for conectado a uma carga de 0,8 ∠ 10 °Ω no lado de baixa tensão, determine as corrente
38. Um transformador de 4,6k V A , 2300 / 115V , 60H z foi projetado para ter uma f . e . m induzida de 2,5V o l t s / e s p i r a . Supondo o transformador ideal, calcule:a) O número de espiras do en
40. O primário de um transformador ideal com relação de espiras igual a 5 é conectado a uma fonte de tensão com parâmetros de T h é v e n i n é V T h = 10c o s2.000 tV e R T h = 100Ω . Determine a pot
42. Considere o circuito da figura 13.107 e determine a potência absorvida pelo resistor de 2Ω . Suponha que 80V seja um valor R M S .