Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 42
42. Para o circuito da figura , determine o equivalente de entre os terminais .
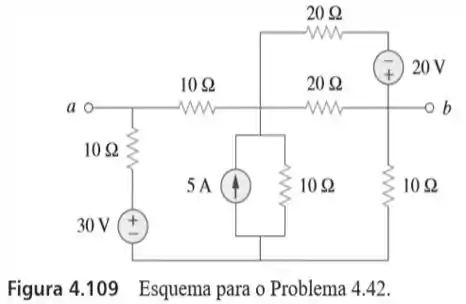
Passo 1
Bom! A primeira coisa que temos que fazer, e encontrar a resistência equivalente nos terminais do resistor . Por isso, vamos ter que redesenhar esse circuito, excluindo as fontes de tensão e de corrente que nele estão presentes.
E aqui está nossa figura:
Essa região azul destacada aí, é uma configuração estrela! Não é legal da gente trabalhar, por isso vamos transformar esse circuito de uma configuração estrela para uma configuração triangular, ou em delta .
Para fazer isso, bora usar as fórmulas abaixo:
Onde podemos ver que há duas resistências de em paralelo. Temos então, os seguintes valores:
E com isso, chegamos aos seguintes resultados:
O nosso circuito, sofre assim, a seguinte transformação:
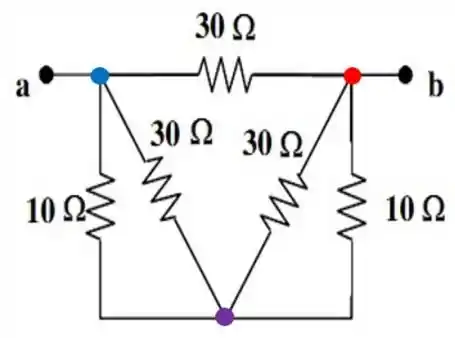
E com isso, podemos ver que a nossa resistência de , é dada por:
Passo 2
Em seguida, o próximo passo é obter a tensão de , .
Olha só! A gente vai fazer isso, através de um método diferente dessa vez; usando a análise de malhas.
Por isso, bora fazer o esboço desse circuito, já nomeando as correntes de malha. Antes disso, temos que fazer a transformação daquelas duas resistências de , que estão em paralelo.
E com isso, chegamos até a seguinte figura...
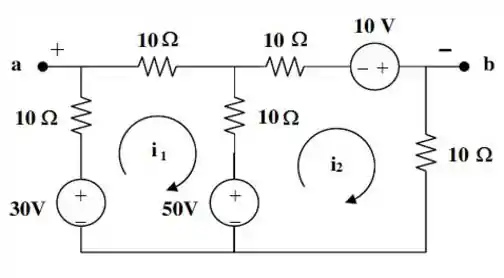
Passo 3
Aplicando a lei das tenões de para a malha , obtemos que....
E depois fazendo o mesmo para a malha , obtemos que....
Chegamos assim, até ao seguinte sistema de equações:
Mutiplicamos por e depois somamos com a equação ... Conseguimos que:
E o valor de é dado por:
Sabe o porquê de termos feito isso?
A resposta está na fgira abaixo:
O motivo, é que percorrendo o caminho abaixo, de até , podemos obter facilmente a nossa tensão de , que nada mais é do que a tensão entre os terminais e . E essa tensão vai valer:
E voilà! Obtemos nossas respostas!