Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 50
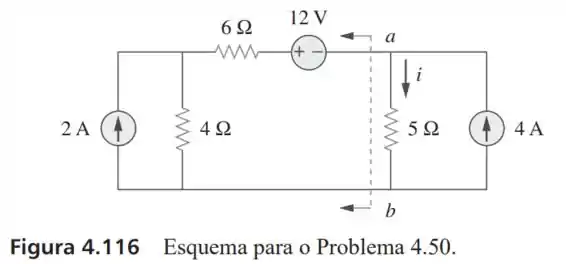
50- Obtenha o equivalente de Norton do circuito da Figura a esquerda dos terminais . Use o resultado para encontrar a corrente .
Passo 1
Fazendo o corte e analisando o circuito a esquerda nós teremos a seguinte análise a fazer.
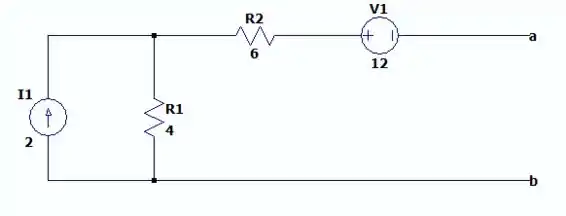
Como as fontes de e de estão com pelo menos um terminal conectadas no vazio, ou seja nos terminais e , isso nos diz que na situação dada na figura acima nenhuma das fontes estará realmente ligada, com isso dito nós podemos arrancar essas fontes fora (por elas não fazerem nada no circuito) e podemos calcular a resistência de Norton da seguinte forma:
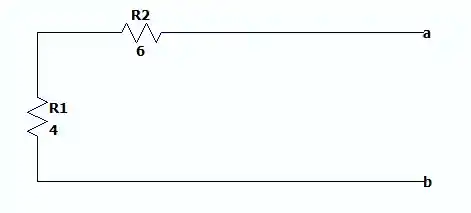
Dessa forma a resistência entre os terminais e (ou resistência de Norton ) será:
Passo 2
Agora vamos fechar o contato em para que possamos calcular a corrente de Norton da seguinte forma.
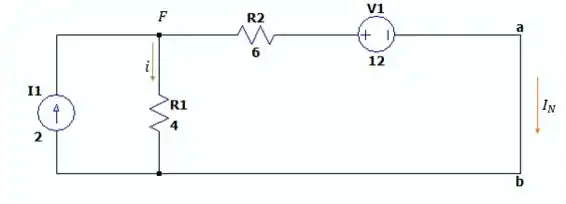
Se fizermos a somatória das correntes que entram e igualarmos com as correntes que saem de nós teremos:
Agora note que temos duas tensões iguais, a que sai de passa pela resistência de e para em e outra que passa pela resistência de e pela fonte de de forma que teremos a seguinte igualdade de tensão.
Pois a corrente está a favor da tensão da fonte de tensão (indo do positivo para o negativo) então o sinal é positivo.
Dessa forma:
O sinal negativo nos diz que o sentido da corrente é para o outro lado, porém vamos conservar o que fizemos para a próxima questão.
Passo 3
Agora vamos utilizar essa fonte de corrente resultante para analisar os circuitos a direita do corte .
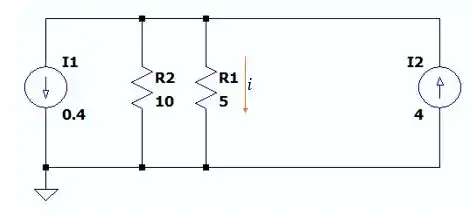
Não devemos esquecer que tem uma resistência a ser transportada também, e ela sempre em paralelo com a fonte de corrente.
Sabendo que a corrente resultante vinda das duas fontes de tensão será:
E com isso a corrente que passará pela resistência de