Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 13
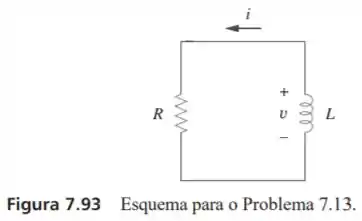
No circuito da figura 7.93,
Determine .
Calcule a energia dissipada na resistência para .
Passo 1
Dadas as equações que foram fornecidas pelo enunciado temos que a constante de tempo é dada pelo inverso do expoente da exponencial presente nas funções. Para nosso caso vamos ter
Aplicando a lei de Ohm para o nosso resistor vamos ter
Agora que temos o valor de e de podemos relacionar esses valores com através da seguinte equação
Passo 2
Por fim, para acharmos a energia dissipada pela resistência no tempo estabelecido basta aplicarmos a seguinte equação
Resposta
Exercícios de Livros Relacionados
A chave no circuito da Figura P7.4 esteve na posição 1 por um longo tempo. Em t = 0 , ela passa instantaneamente para a posição 2. Determine v o t para t ≥ 0 + .
A chave no circuito da Figura P7.10 esteve na posição 1 por um longo tempo. Em t = 0 , ela passa instantaneamente para a posição 2 . Determine o valor de R de modo que 10 % da energia inicial armazena
As duas chaves no circuito visto na Figura P7.6 são sincronizadas. Elas estiveram fechadas por um longo tempo antes de se abrirem em t = 0 .a) Em quantos microssegundos, depois da abertura das chaves,
No circuito da Figura P7.7, a chave esteve fechada por um longo tempo antes de ser aberta em t = 0 .a) Determine o valor de L de modo que v 0 t seja igual a 0,5 v 0 0 + quando t = 1m s .b) Determine a
A chave mostrada na Figura P7.9 esteve aberta durante um longo tempo, antes de seu fechamento em t = 0 .a) Determine i 0 0 - , i L 0 - e v L 0 - .b) Determine i 0 0 + , i L 0 + e v L 0 + .c) Determine