Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 7.Problemas - Ex. 4

A chave no circuito da Figura P7.4 esteve na posição 1 por um longo tempo. Em t = 0 , ela passa instantaneamente para a posição 2. Determine v o t para t ≥ 0 + .

Passo 1

t

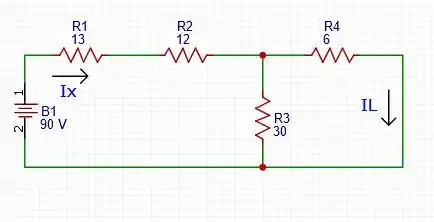
Para i x , basta fazer a resistência equivalente:

i x = 90 13 + 12 + ( 6 | 30

i x = 3   A  

Para o caso de i L ( 0 - ) , basta fazer um divisor de corrente

i L 0 - =   30 36 3 = 2.5   A

t > 0 - O circuito se comportará da seguinte forma:

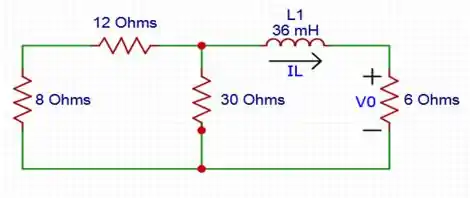
No caso da resistência equivalente, temos o seguinte cálculo:

R e = 6 + 30 | | 8 + 12  

R e = 6 + 12 = 18   Ω

Passo 2

Para a constante de tempo, já temos todas as informações necessárias para fazer o cálculo:

τ = L R e = 36 × 10 - 3 18 = 2   m s

1 τ = 1 2 × 10 - 3 = 500  

Logo,

i L = 2.5 e - 500 t   A

Passo 3

Aplicando a famosa Lei de Ohm ( V = R I )   para v 0 , temos:

v 0 = 6 i 0

v 0 = 15 e - 500 t   V ,   t ≥ 0 +

Resposta

v 0 = 15 e - 500 t   V ,   t ≥ 0 +

Exercícios de Livros Relacionados

8.30) Calcule v1 para t0, se não existe energia inicial armazenada.
8.38) Calcule v para todo t, se (a) vg = 12u(t) V e (b) vg = 12[u(t)-u(t-1)]V.
Para o circuito da Figura P7.72, em quantos milissegundos, após a chave 1 passar a posição b, a energia armazenada no indutor é 4% de seu valor inicial?