Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas - Ex. 26

Para o circuito da figura 2.90 , i 0 = 3 A . Calcule i x e a potência total dissipada pelo circuito.

Passo 1

Dá uma olhadinha no circuito:

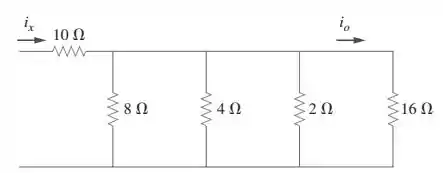
Aqui nessa situação, temos vários resistores em paralelo, sendo eles os de 8 Ω , 4 Ω , 2 Ω e 16 Ω . Mas o que significa esse paralelo dos resistores? Que a tensão sobre todos eles é igual! Assim, podemos escrever:

16 i 0 = 2 i 2 = 4 i 4 = 8 i 8

Sendo i 2 a corrente que passa no resistor de 2 Ω , i 4 a do resistor de 4 Ω e i 8 a do resistor de 8 Ω . Como i 0 = 3 A , vamos descobrir essas correntes!

2 i 2 = 16 × 3 → i 2 = 24 A

4 i 4 = 16 × 3 → i 4 = 12 A

8 i 8 = 16 × 3 → i 8 = 6 A

Passo 2

Belezura, encontramos a corrente que passa em cada um dos resistores em parelelo. Pela lei de Kirchoff das correntes, a corrente que entra em um nó é a mesma que sai por esse nó. Daí, como a gente pode ver pelo desenho, essa corrente i x se dividiu em todas essas outras correntezinhas, então:

i x = i 0 + i 2 + i 4 + i 8

i x = 3 + 24 + 12 + 6

i x = 45 A

Passo 3

Pra fechar, queremos a potência total dissipada no circuito. Cada resistor dissipa uma corrente de R i 2 , então é só a gente calcular isso tudo e somar!

P = 10 i x 2 + 8 i 8 2 + 4 i 4 2 + 2 i 2 2 + 16 i 0 2

Substituindo,

P = 10 45 2 + 8 6 2 + 4 12 2 + 2 24 2 + 16 3 2

Então,

P = 22410 W

Resposta

i x = 45 A

P = 22410 W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule I 0 no circuito da figura 2.91 .
Determine a R e q para o circuito da figura 2.94 .
Usando associações de resistências em série/paralelo, determine a resistência equivalente vista pela fonte no circuito da figura 2.98 e a potência total dissipada pela rede de resistores.
Determine R para o circuito da figura 2.101 .
Todos os resistores na figura 2.93 são de 5 Ω cada. Determine R e q .