Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas - Ex. 34
Usando associações de resistências em série/paralelo, determine a resistência equivalente vista pela fonte no circuito da figura e a potência total dissipada pela rede de resistores.
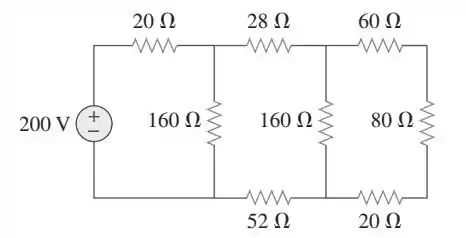
Passo 1
Bora lá, galera, dá uma analisada no circuito.
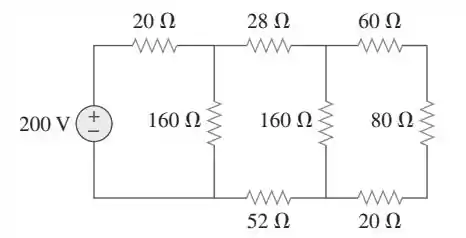
Acompanha comigo: lá na direita, os resistores de , e estão todos em série, correto? Eles tem a resistência equivalente de:
Esses três resistores estão em paralelo com o resistor de . Resolvendo esse paralelo, vão ser equivalentes a:
Passo 2
Vamos ficar com:
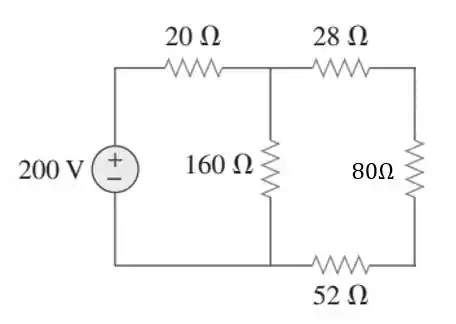
Agora, os resistores de , e estão em série, dando um total de:
E esses também estão em paralelo com o de , dando de novo um equivalente de .
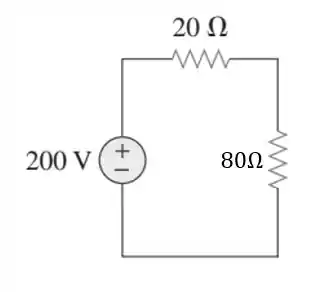
Daí, esse de vai ficar em série com o de , gerando a nossa do circuito todo:
Passo 3
Daí a gente consegue encontrar a corrente que passa pelo circuito!
Então a potência total do circuito vai ser:
Assim,