Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas - Ex. 13
Para o circuito da figura , use a LKC para encontrar as correntes nos ramos a .
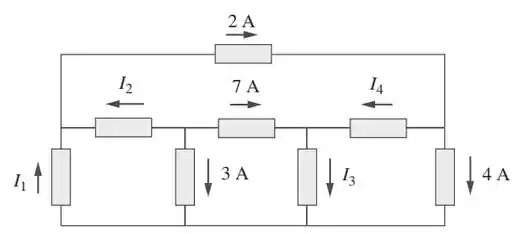
Passo 1
Dá uma olhadinha no circuito:
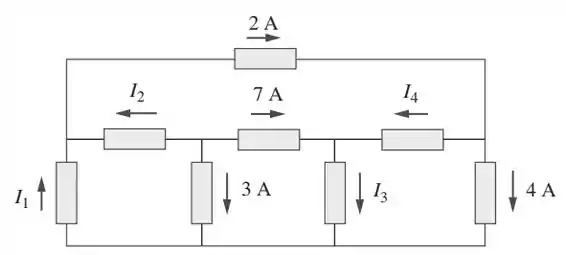
Para resolver essa questão, vamos usar a lei de Kirchoff para correntes, que diz que a corrente total que entra em um nó tem que ser a mesma que sair dele!
Passo 2
No ramo em que temos , e , as três estão saindo do nó e nenhuma entrando, por isso:
Agora, na esquerda, temos e se juntando para dar :
Lá na direita, essa corrente de se divide em e :
Pra fechar, e estão se juntando para dar .
Resposta
Exercícios de Livros Relacionados
Na Figura 3.3, calcule a resistência vista pela fonte (isto é, olhando pelos terminais a-b)se: a) R 1 = 1,50Ω e R 2 = 2Ω b) R 1 = R 2 = 0,1Ω .
No gráfico do circuito do Problema 4.8, selecione a arvore das fontes de tensão e 0 resistor de 12Ω . Empregando o método desta seção, escreva uma equação da LKC e caIcule v
No gráfico do circuito do Problema 4.8, selecione a arvore das fontes de tensão e o resistor de 12 Ω . Empregando o método desta seção, escreva uma equação da LKC e caIcule v.
Considere o circuito mostrado na Figura P2.17. a) Determine v 0 usando as leis de Kirchhoff e a lei de Ohm. b) Teste a solução para v 0 , verificando que a potência total fornecida é igual à potência
a) Determine as correntes i 1 e i 2 no circuito da Figura P2.19. b) Determine a tensão v 0 . c) Verifique que a potência total fornecida é igual à potência total consumida.