Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 5.Problemas - Ex. 24

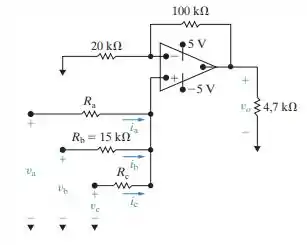
O circuito da Figura P5.24 é um amplificador somador não inversor. Admita que o amp op seja ideal. Projete o circuito de modo que v o   =   v a   +   2 v b   +   3 v c   .

a) Especifique os valores de R a   e   R c .

b) Calcule i a, i b e i c (em microampères), quando v a   =   0,7   V ,   v b   =   0,4   V   e   v c   =   1,1   V .

Passo 1

E ai seres de luz, tudo bem?

Bora resolver mais uma?

Encostaaa!!

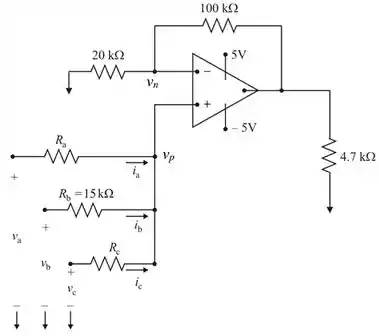
Redesenhe o circuito como mostrado na Figura 1

Passo 2

  1. O amplificador operacional é ideal

    2. v o = v a + 2 v b + 3 v c       1

    Use o teorema da superposição e primeiro remova as entradas de tensões v b   e   v c do circuito, ou seja, v b = 0   e   v c = 0 .

    Iremos usar a regra da divisão de tensão para calcular a tensão v p a devido à entrada v a .

    v p a = v a ( R b | R c R a + ( R b | R c          

    = v a R b R c R b + R c R a + R b R c R b + R c

    = v a R a R b R a R b + R c + R b R c

    = v a R a R b R c R a R a R b + R b R c + R c R a  

    Simplifique ainda mais

    v p a = v a R a k             ( 2 )

    Onde

    k = R a R b R c R a R b + R b R c + R c R a

    Passo 3

    A tensão v p b devido à entrada v b e a tensão devida v p c à entrada v c são semelhantes à tensão v p a devida à entrada v a ou seja,

    v p b = v b R b k         3

    v p c = v c R c k         4

    A tensão v p é a soma das tensões v p a ,   v p b   e   v p c  

    v p = v p a + v p b + v p c

    v p = v a R a k + v b R b k + v c R c k

    = k v a R a + v b R b + v c R c         ( 5 )

    Como o amp-op é ideal, a tensão no terminal inversor v n é igual à tensão no terminal não inversor ( v p ) , ou seja,

    v n = v p

    v n = k v a R a + v b R b + v c R c

    Passo 4

    Aplicando a lei das correntes de Kirchhoff no nó v n

    0 - v n 20 × 10 3 = v n - v o 100 × 10 3

    v n 10 3 1 20 + 1 100 = v o 100 × 10 3

    v o = 6 v n

    Substituindo

    v o = 6 k v a R a + v b R b + v c R c           ( 6 )

    Passo 5

    Comparando a expressão (1) e a expressão (6)

    6 k R b = 2

    k = 2 R b 6

    k = R b 3

    Substituindo

    k = 15 × 10 3 3

    k = 5   k Ω

    Comparando a expressão (1) e a expressão (6)

    6 k R a = 1

    Substituindo

    6 5 × 10 3 R a = 1

    R a = 30 k Ω

    Comparando a expressão (1) e a expressão (6)

    6 k R c = 3

    Substituindo

    6 5 × 10 3 R a = 3

    R c = 10   k Ω

    Portanto, o valor de R a = 30   k Ω ,   e   R c   é   10   k Ω .

    Passo 6

  2. Substituindo 0.7   V   p o r   v a ,   0.4   V   p o r   v b ,   1.1   V   p o r   v c ,   5 k Ω   p o r   k ,   30 k Ω   p o r   R a ,   15 k Ω   p o r   R b ,   e   10   k Ω   p o r   R c na expressão 5

v p = 5 × 10 3 0.7 30 × 10 3 + 0.4 15 × 10 3 + 1.1 10 × 10 3

= 0.7 6 + 0.4 3 + 1.1 2

= 0.8   V

A corrente i a é representada da seguinte maneira

i a = v a - v p R a

i a = 0.7 - 0.8 30 × 10 3

= - 3.33   μ A

A corrente i b é representada da seguinte maneira

i b = v b - v b R b

i b = 0.4 - 0.8 15 × 10 3

= - 26.67   μ A

A corrente i c é representada da seguinte maneira

i c = v c - v p R a

i c = 1.1 - 0.8 10 × 10 3

= 30   μ A

Resposta

  1. Portanto, o valor de R a = 30   k Ω ,   e   R c   é   10   k Ω .
  2. Portanto, o valor i a = - 3.33   μ A ,   i b = - 26.67   μ A   e   i c = 30 μ A .

Exercícios de Livros Relacionados

O amp op no circuito da Figura P5.23 é ideal. a) Qual é a configuração desse circuito amp op? b) Determine vo em termos de vs . c) Determine a faixa de valores para vs tal que vo não sature e o amp op
Selecione os valores de R aeR f no circuito da Figura P5.31 de modo que v o=8.000 ( i b-i a ) Use resistores individuais ou combinações de resistores do Apêndice H. O amp op é ideal
O circuito amp op aditivo-subtrativo mostrado na Figura P5.30 é ideal. a) Determine v o quando v a=1V ,v b=2V ,v c=3Vev d=4V . b) Se v a ,v bev d forem mantidas constantes, quais valores de v c não sa
Os resistores no amplificador diferencial mostrado na Figura 5.15 são Ra = 24 kV, Rb = 75 kV, Rc = 130 kV e Rd = 120 kV. Os sinais de entrada de va e vb são 8 e 5 V, respectivamente, e VCC = ± 20 V.a)