Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 7.Problemas - Ex. 56

O circuito da Figura P7.56 está em operação por um longo tempo. Em t = 0, a fonte de tensão inverte a polaridade e a fonte de corrente cai de 3 mA para 2 mA. Determine vo (t) para t $ 0.

Passo 1

Para t < 0 :

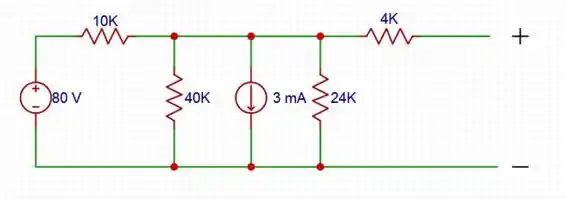
Simplificando o circuito, temos

i * 0 - = 80 10000 = 8   m A

E para a resistência equivalente:

R t h = 1 10 k Ω + 1 40 k Ω + 1 24 k Ω - 1 = 6   k Ω

Logo, no caso da corrente, observe que ela será a diferença entre a corrente encontrada e a fonte de corrente.

i 0 - = 8   m A - 3   m A = 5   m A

Logo, a tensão é igual a:

v 0 0 - = 5 × 10 - 3 6000 = 30   V

Então, o circuito simplificado será da seguinte forma:

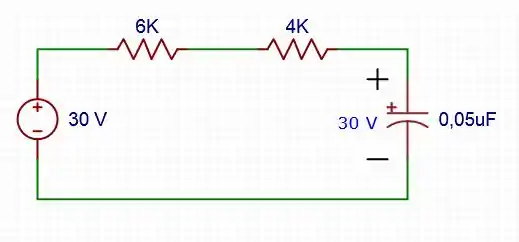
Passo 2

Para t > 0 : A fonte de corrente decai para 2   m A , logo, o circuito se comporta da seguinte forma

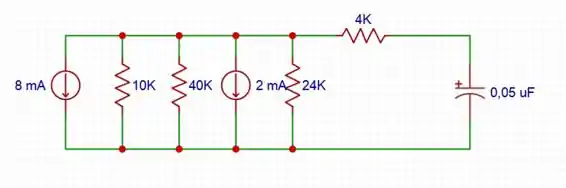
Simplificando o circuito, temos:

I = 8   m A + 2   m A = 10   m A

R t h = 1 10 k Ω + 1 40 k Ω + 1 24 k Ω - 1 = 6 k Ω

A tensão é igual a:

V = 10 × 10 - 3 6000 = 60   V

Logo, o circuito simplificado será igual a:

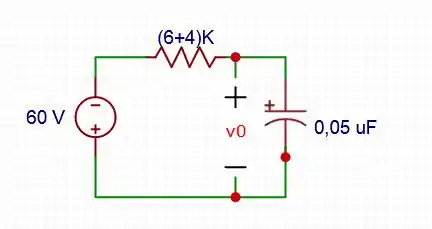
Logo, para o caso do circuito se estabilizar durante muito tempo, temos:

v 0 ∞ = - 10 × 10 - 3 6 × 10 - 3 =   - 60   V

Com isso, também já se pode calcular a constante de tempo:

τ = R C = 10000 0,05 × 10 - 6 = 0,5   m s

E a sua inversa:

1 τ = 2000

Agora, utilizando a equação geral, temos:

v 0 = v 0 ∞ + v 0 0 + - v 0 ∞ e - t / τ  

Substituindo os valores:

v 0 = - 60 + 30 - - 60 e - 2000 t

v 0 = - 60 + 90 e - 2000 t   V ,     t ≥ 0

Resposta

v 0 = - 60 + 90 e - 2000 t   V ,     t ≥ 0

Exercícios de Livros Relacionados

Esboce a tensão dada por: v t = t u t - 2 t - 1 u t - 1 + t - 2 u t - 2 v
Calcule vs ev g = 5 e - t u t V e não existe energia inicial armazenada. (Este circuita é como o integrador da figura 8.24, exceto que o capacitor tem um resistor em paralelo com ele, tornando-o um ca
CaIcule i no Ex. 8.8.1, se i g = 10 u t - u t - 1 A
Calcule as respostas ao degrau iev [ i g = u t A ] .
Reduza (8.22) a forma de (8.23) v t = 12 1 - e - t u t - u t - 1 + 12 1 - e - t e - t - 1 u ( t - 1 ) Em, v t = 12 1 - e - t u t - 12 ( 1 - e - t - 1 ) u ( t - 1 )