Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.Problemas - Ex. 6
Se um circuito está em regime permanente em , calcule para .
Passo 1
Iae, meus queridos! Td certinho?
Essa questão é bem tranquila. Bora lá!
No instante , o circuito está em regime permanente, dessa forma, podemos considerar o circuito da seguinte maneira:
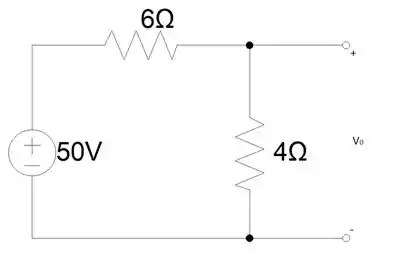
A tensão no capacitor será a mesma tensão do resistor de 4Ω, então vamos calcular essa tensão aplicando a Lei de Ohm na malha:
Calculando :
Passo 2
Para , o circuito terá a seguinte forma:
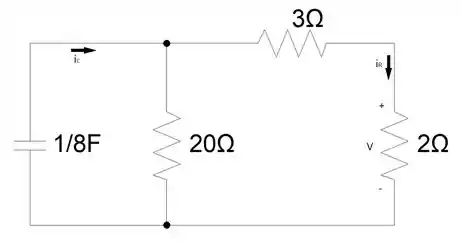
Vamos calcular o desse circuito para gerarmos a equação de tensão do capacitor .
Formulando a equação
Agora temos que calcular :
Aplicando a regra de divisão de corrente para calcular :
Finalmente, por fim, aplicar Lei de Ohm e vai aparecer magicamente:
Foi tranquilo? Toma uma água e bora pra outra!
Resposta
Exercícios de Livros Relacionados
O capacitor no circuito mostrado na Figura P7.87 está carregado com 20 V, no instante em que a chave é fechada. Se o dielétrico do capacitor se rompe (perde suas características isolantes) quando a te
Não há nenhuma energia armazenada no capacitor do circuito da Figura P7.77 quando a chave 1 se fecha em t = 0. A chave 2 fecha‑se 2,5 milissegundos mais tarde. Determine vo(t) para t $ 0.
A chave no circuito da Figura P7.80 esteve na posição a por um longo tempo. EM t=0, ela passa instantaneamente para a posição b, onde permanece por 5 segundos antes de passar instantaneamente para a p