Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.Problemas - Ex. 12
Calcule para , se o circuito está em regime permanente em .
Passo 1
Iae, meus queridos! Td certinho?
Essa questão pode ser um pouco trabalhosa, mas nada do que não podemos tirar de letra!
Quando , o circuito tem a seguinte cara.
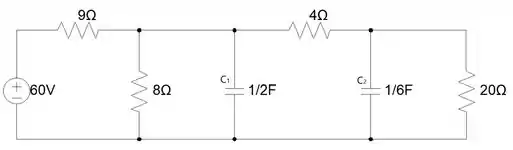
No instante , podemos considerar os capacitores, como um circuito aberto já que a questão nos disse que o circuito está em regime permanente.
Esse circuito vai nos servir para calcularmos os valores das tensões iniciais de e . A tensão em está fácil, é a mesma tensão no resistor de 20Ω, já a tensão em será a soma das tensões dos resistores de 20Ω e 4Ω. Entendeu?
Vamos calcular a corrente gerada pela fonte usando a resistência equivalente do circuito. Já sabemos calcular resistência equivalente de circuitos, então vamos dar uma enxugada nessa parte.
Aplicando a regra de divisão de correntes, vamos calcular a corrente que passa nos resistores de 20Ω e 4Ω.
Dessa forma, a tensão no resistor de 20Ω é 20V e no resistor de 4Ω é 4V, ou seja, a tensão em é 24V e a tensão em é 4V.
Td certo até agora? 👍
Passo 2
Para o tempo , o circuito terá a sente cara.
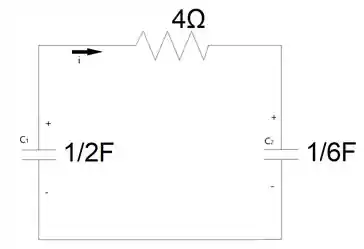
Relembrando: e .
Vamos calcular a associação dos capacitores e formular a equação geral de tensão para circuitos RC.
Já com as tensões, vamos calcular a diferença entre elas. Por simetria ao sentido da corrente , vamos fazer . Portanto
A equação será:
Por fim, aplicamos a Lei de Ohm para surgir a equação da corrente para
Iae, foi tranquilo? Não pare agora, bora pra mais uma!