Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 13.Problemas - Ex. 86

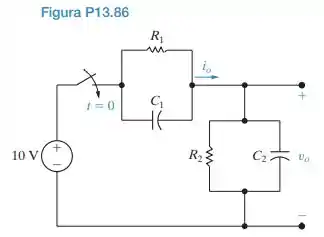
A combinação em paralelo de R2 e C2, no circuito da Figura P13.86, representa o circuito de entrada de um osciloscópio analógico. A combinação em paralelo de R1 e C1 representa o cabo de compensação, que é usado para ligar a fonte de sinal ao osciloscópio. Não há nenhuma energia armazenada em C1 ou em C2 no momento em que a fonte de 10 V é ligada ao osciloscópio, por meio do cabo de compensação. Os valores do circuito são C1 = 4 pF, C2 = 16 pF, R1 = 1,25 M Ω e R2 = 5 M Ω .

a) Determine vo.

b) Determine i o .

c) Repita (a) e (b), quando C1 for alterado para 64 pF.

Passo 1

Falaaa, pessoal! Como vocês estão?

Bora pra mais uma questãozinha pra exercitar o que a gente sabe sobre a transformada de Laplace na análise de circuitos!

  1. Analisando o circuito acima, temos:

    2. Z 1 = 1 / C 2 s + 1 / R 1 C 1 = 25 x 10 10 s + 20 x 10 4 Ω

    Z 2 = 6,25 x 10 10 s + 12500 Ω

    Também sabemos que:

    V 0 Z 2 + V 0 - 10 / s Z 1 = 0

    Logo:

    V 0 = 2 ( s + 200000 ) s ( s + 50000 )

    O que em termos de K, nos dá:

    K 1 = 2 200000 50000 = 8 ; K 2 = - 6

    Portanto:

    v 0 = 8 - 6 e - 50000 t u t V

    Passo 2

  2. Temos que:

    3. I 0 = V 0 Z 2 = 2 ( s + 200000 ) ( s + 12500 ) s s + 50000 25 x 10 10

    O que em termos de K, nos dá:

    K 1 = 50000 ; K 2 = 112500

    Portanto:

    i 0 = 32 δ t + 1,6 x 10 6 + 3,6 x 10 6 e - 50000 t u t p A

  3. Quando C1=64 pF, temos que:

Z 1 = 156,25 x 10 8 s + 12500 Ω

Também sabemos que:

V 0 + 4 V 0 = 40 s

Logo:

v 0 = 8 u t V

I 0 = V 0 Z 2 = 128 x 10 - 12 1 + 12500 s

Logo:

i 0 t = 128 δ t + 1,6 x 10 6   u t p A

Resposta

  1. Item a:

    2. v 0 = 8 - 6 e - 50000 t u t V

  2. Item b:

    3. i 0 = 32 δ t + 1,6 x 10 6 + 3,6 x 10 6 e - 50000 t u t p A

  3. Item c:

v 0 = 8 u t V

i 0 t = 128 δ t + 1,6 x 10 6   u t p A

Então é isso, pessoal! Nos vemos na próxima questão. 😊

Exercícios de Livros Relacionados

O amp op no circuito mostrado na Figura P13.47 é ideal. Não há nenhuma energia armazenada nos capacitores no instante em que o circuito é energizado. Determine (a) Vo, (b) vo e (c) quanto tempo o amp
Um pulso de tensão retangular, v i=[ u ( t )-u ( t-1 ) ]V , é aplicado ao circuito da Figura P13.59. Use a integral de convolução para determinar vo.