Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 3.Problemas - Ex. 26
Conecte uma fonte de corrente de entre os terminais a-b na Figura 3.9(a), com a seta da corrente apontando para cima.
a) Use a divisão de corrente para determinar a corrente no resistor de , de baixo para cima.
b) Use o resultado da parte (a) para determinar a tensão no resistor de , positiva na parte superior.
c) Use o resultado de (b) e a divisão de tensão para determinar a tensão nos terminais do resistor de , positiva na parte superior.
d) Use o resultado de (c) e a divisão de tensão para determinar a tensão nos terminais do resistor de , positiva na parte superior.
Passo 1
Show de bola, galera! Vamos dar sequência ao que estamos fazendo. Para isso, vamos colocar abaixo a figura que foi citada no enunciado:
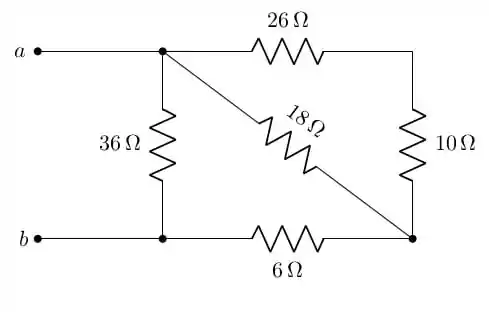
Além disso, vamos ligar uma fonte de corrente entre os pontos a e b, assim, o circuito que iremos analisar será:
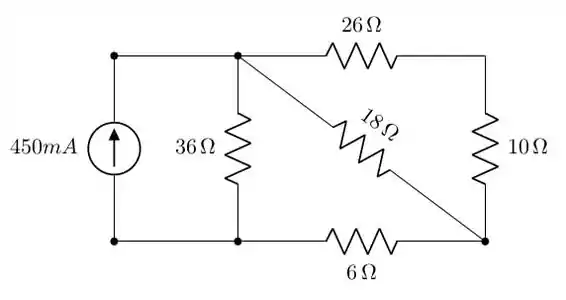
Passo 2
a)
Reduzindo o circuito, ficaremos com as seguintes topologias:
Primeiro faremos a associação série dos resistores de e :
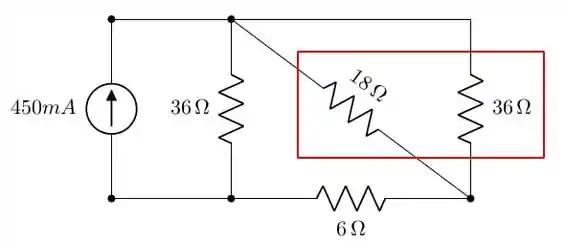
A imagem acima já nos mostra o próximo passo: iremos fazer o equivalente paralelo dos resistores destacados:
A nova topologia será:
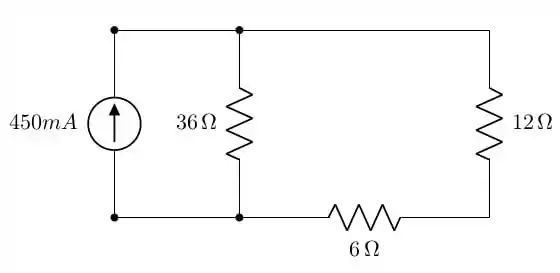
Esse circuito será simplificado e teremos o seguinte:
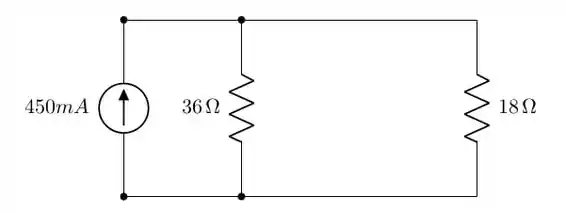
De posse desse circuito simplificado, podemos aplicar o divisor de corrente:
Passo 3
b)
O que temos que fazer aqui é simplesmente aplicar a Lei de Ohm:
Passo 4
c)
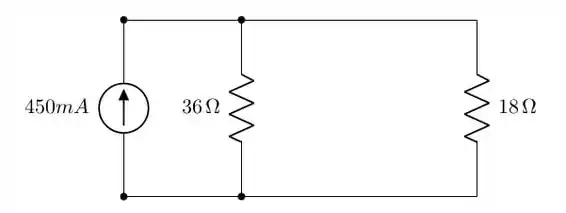
Da figura, percebemos que os dois resistores estão em paralelo, logo, possuem a mesma tensão. Assim,
No entanto, não é este resistor de que o enunciado se refere, mas o do circuito abaixo:
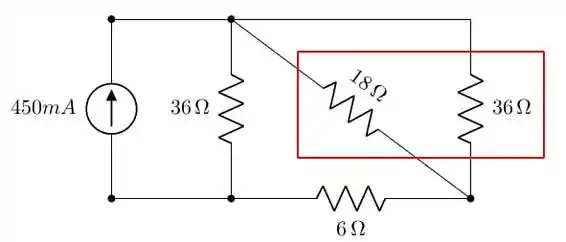
Se observarmos bem, esse resistor de foi associado em paralelo com o de . Sendo assim, a tensão em cima do resistor resultante também será a tensão nesses dois resistores. Para sabermos qual foi o resistor, vamos repetir a seguinte figura
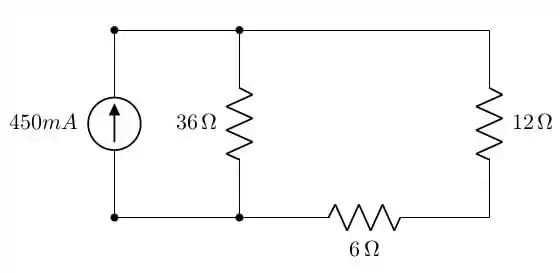
Assim, vamos calcular a tensão em cima do resistor de
Logo, este é o valor procurado.
Passo 5
d)
Como explicado no passo anterior, a tensão no resistor equivalente de é a mesma no resistor original de e na associação série de . Então iremos focar nesta associação série.
Agora, vamos comer uma goiabada pra ganhar energia e irmos à próxima questão.
Resposta
a)
b)
c)
d)