Examine o circuito da Figura P3.7(a).
a) Use a divisão de tensão para determinar a queda de tensão nos terminais do resistor de , positiva à esquerda.
b) Usando o resultado de (a), determine a corrente que percorre o resistor de , da esquerda para a direita.
c) Usando o resultado de (b), utilize a divisão de corrente para determinar a corrente no resistor de , de cima para baixo
d) Usando o resultado de (c), determine a queda de tensão nos terminais do resistor de , positiva na parte superior.
e) Usando o resultado de (d), utilize a divisão de tensão nos terminais do resistor de , positiva na parte superior.
Passo 1
Uooooooooooooou!
Vamos dar início a mais uma questão e como ela está fazendo referência a uma figura de uma questão anterior, vamos colocar o desenho aqui para você não precisar voltar as páginas do livro, meu xuxuzinho!!!
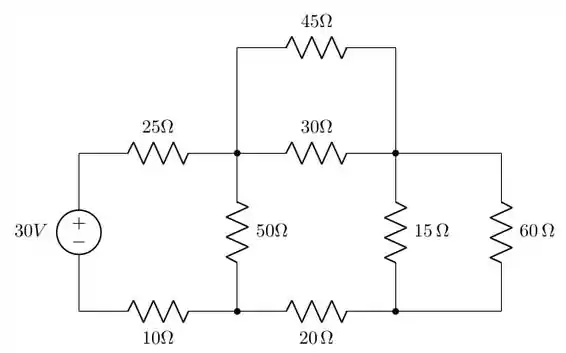
Passo 2
a)
Vamos começar simplificando este circuito fazendo 2 cálculos de resistores em paralelo:
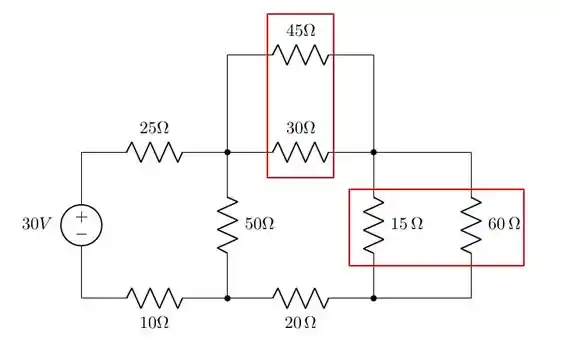
e
Redesenhando o circuito, obtemos:
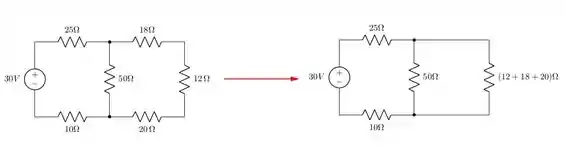
Depois de tantos desenhos e simplificações, podemos finalmente aplicar o método ao circuito dado:
Passo 3
b)
Esse item foi dado. Tudo o que temos que fazer aqui é usar a Lei de Ohm:
Passo 4
c)
A corrente que circula no resistor de é a mesma que circula na malha que contém a fonte. No entanto, à medida que expandimos o circuito, temos que analisar como ficam as divisões de corrente:
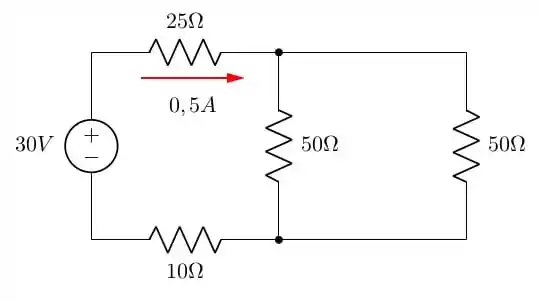
Como temos 2 resistores iguais, a corrente irá se dividir igualmente, assim, a corrente vale:
Passo 5
d)
Novamente, aqui vamos só aplicar a Lei de Ohm:
Passo 6
e)
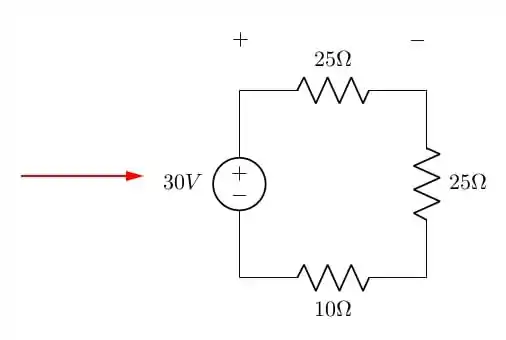
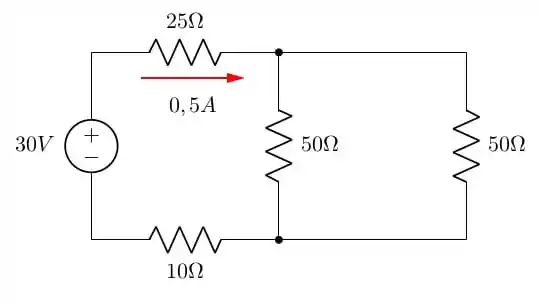
Para visualizarmos melhor, vamos utilizar 3 figuras. A primeira é a da divisão de corrente em 2 partes iguais, utilizada na letra c):
Agora vamos expandir esta figura nos componentes à direita:
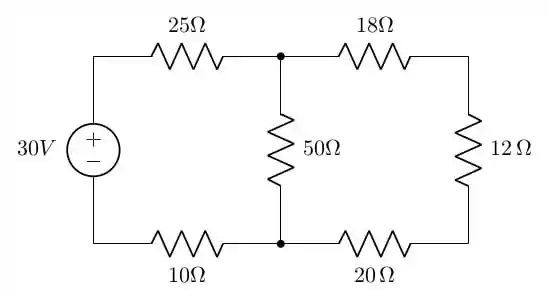
Sabemos que a corrente de circula pelo ramo do resistor de e outros circula no ramo composto pelos 3 resistores em série. Assim, podemos calcular a queda de tensão em cada resistor separadamente. O resistor de interesse no nosso caso é o de :
Finalmente, vamos usar nossa terceira figura:
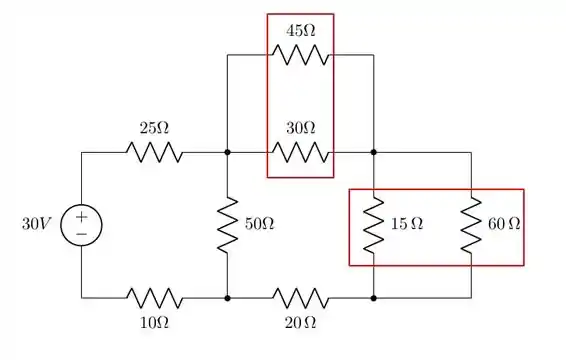
A tensão no resistor de é a mesma nos resistores em paralelo ( e ). Logo:
Ufa! Essas questões são simples, mas dão muito trabalho. Bora beber uma água antes de irmos para a próxima.
Resposta
a)
b)
c)
d)
e)